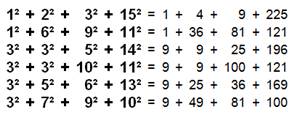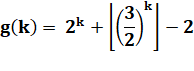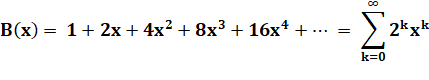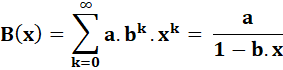NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/08/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ADDITION
Débutants Addition	PARTITION				Glossaire Addition
Rubrique PARTITION	Entiers & Carrés	Cubes		Puissances 4...n
	Somme de 4 carrés Théorème de Lagrange		Somme de n puissances Théorème de Waring
	1 à 100 en 4 carrés
	Sommes de cubes et autres puissances
	Comprendre les sommes de carrés
	Théorème de Richert – Partition sous contrainte de poids
	Sommaire de cette page >>> Approche >>> Somme de R puissances K: théorème de Waring >>> Somme de carrés non nuls >>> Somme de R puissances K donnant une puissance k >>> Somme de 2 puissances K donnant une puissance k >>> Somme de puissances différentes >>> Factorielles >>> Produits de puissances

Théorème de Waring

Un nombre est toujours la somme d'au plus

4 carrés

9 cubes

…

r puissances k

Généralisation du théorème de Lagrange:

Tout nombre est la somme d'au plus quatre carrés.

Bonus: florilège de curiosités avec les sommes de puissances

Anglais: Waring's problem

Voir Euler et Fermat 

Approche avec le nombre 239
Tout entier est décomposable en somme d'au plus
4 carrés	9 cubes	19 puissances quatrièmes
Il faut quatre carrés pour faire 239, pas moins. Par contre, il existe six façons de faire:	Les deux seuls nombres qui nécessitent les neuf cubes sont : 23 et 239	239 est l'un d'eux
	23 = 2 x 2^3 + 7 x 1^3 239 = 2 x 4^3 + 4 x 3^3 + 3 x 1^3

SOMME de r PUISSANCES k
Théorème de Waring (1770) Il existe toujours une somme limitée de puissances pour tous les nombres et pour toutes les puissances: N = a1^k + a2^k + … + ar^k Dit autrement: r , la quantité de termes de la somme, n'est jamais infini.	Du temps d'Edward Waring (1734-1798), c'était une hypothèse. Complètement démontré en 1985. David Hilbert avait montré que la somme est limitée.

Voir Contemporains

Entier n = somme de:
r	k	Découverte	Date
3	triangulaires	Fermat, Gauss	1638
4	carrés	Lagrange	1770
9	cubes	Wieferich et Kempner	1910
19	puissances 4	R. Balasubramanian, Deshouillers et Dress	1986
37	puissances 5	Chen	1964
73	puissances 6	Pillai	1940
143	puissances 7	Heilbronn	1936
279	puissances 8
548	9
1 079	10
2 132	11	Conjecture Les crochets "bas" demandent à prendre la valeur plancher. Exemple
4 223	12
8 384	13
16 673	14
33 203	15
66 190	16
132 055	17
263 619	18
526 502	19
1 051 899	20
r	puissances k	Hardy et Littlewood	vers 1935

Note: Découvertes, pas forcément démontrées

Somme de carrés non nuls

Le théorème de Lagrange (Waring pour les carrés) dit que quatre carrés, au plus, suffisent pour partitionner tout nombre entier.

En faisant la somme avec quatre carrés, certains termes sont nuls, comme 6 = 2² + 1 + 1 + 0. Combien faut-il de termes pour couvrir les entiers, mais sans autoriser le 0?

Réponse: 5 termes, et cela à partir de 34.

Tout nombre > 33 est la somme de cinq carrés non nuls.

Il faut atteindre 60 pour que tout nombre supérieur soit deux fois la somme de cinq carrés non nuls.

61 = 6² + 5² = 6² + 4² + 3² = 5² + 4² + 4² + 2² = 7² + 2² + 2² + 2²

Somme de R puissances K donnant une puissance K

Conjecture d'Euler (fausse!) Aucune puissance k-ième ne peut être décomposée en somme de moins de k puissances k-ièmes. C'est vrai pour les cubes: un cube n'est pas la somme de deux cubes. Mais, par exemple, pour la puissance 5: 144^5 = 27^5 + 84^5 + 110^5 + 133^5 L. J. Lander et T. R. Parkin en 1966 Pour la puissance quatre, il a fallu attendre les ordinateurs. La solution avec des entiers les plus petits serait: 95 800^4 + 7 517^4 + 414 560^4 = 422 560^4  Roger Frye par ordinateur La première solution trouvée était: 2 682 440^4 + 15 365 639^4 + 18 796 760^4 = 20 615 673^4 Noam Elkies en 1988 Aucun contre-exemple connu pour n > 5. Leonhard Euler (1707-1783) Il avait conjecturé que la somme de trois bicarrés ne pouvait pas être un bicarré. Autrement dit, L'équation suivante n'a pas de solution: x^4 + y^4 + z^4 = w^4 En 1988 L'Américain Noam Elkies a trouvé une solution en utilisant un ordinateur et... une étude théorique poussé. La solution en 422 560 de Roger Frye est la seule inférieure à 1 million. Mais au-delà, il y a une infinité de solutions!

Voir Puissance 4 / Euler

Nombre r de puissances k donnant une puissance k
k	r
2	2
3	3
4	3
5	4 au plus, peut-être 3, on ne sait pas.
…
n	2^n

Somme de deux puissances k

donnant presque une puissance k

Grand théorème de Fermat

Pour n > 2, n à la puissance k, ne peut pas être décomposé en somme de deux nombres à la puissance k.

Voir Théorème de Fermat-Wiles / Fermat

Presque Fermat en puissance de trois

x³ + y³ = z³ = 1 ou – 1

6³ + 8³ = 9³ – 1

9³ + 10³ = 12³ + 1

720³ + 242³ = 729³ – 1

729³ + 244³ = 738³ + 1

Presque Fermat en puissance de quatre

On ne connaît pas de solution à: x⁴ + y⁴ = z⁴ 1

Consécutifs

Nombres consécutifs en étant des puissances parfaites.

3^2	–	2^3	=	1	Ce cas est le seul cas de puissances consécutives connu
9	–	8	=	1
x^m	–	y^n	=	1	N'a qu'une seule solution Conjecture de Catalan (1844)
x^m	,	y^n	et	z^p	Ne sont jamais des nombres consécutifs. Démontré par W.J. Lévèque (1952)

On a démontré que trois nombres consécutifs ne peuvent pas être des puissances parfaites.

Pour deux nombres consécutifs, on n'a pas d'exemple (sauf 8, 9), mais le cas général n'est pas démontré.

Somme de puissances

SOMME DE 2 PUISSANCES IDENTIQUES Seul le nombre parfait 28 est la somme de deux puissances identiques: 28 = 1^3 + 3^3 SOMME DE 2 PUISSANCES DIFFÉRENTES Seuls deux nombres sont décomposables en somme de puissances successives en partant de un: 31 = 1 + 5 + 5² 8 191 = 1 + 2 + 2² + 2^3 +...+ 2^12 Nombre, somme de puissances successives de ses chiffres 135 = 1^1 + 3^2 + 5^3 175 = 1^1 + 7^2 + 5^3 518 = 5^1 + 1^2 + 8^3 598 = 5^1 + 9^2 + 8^3 Carré, somme des puissances successives Seul un carré est décomposable en somme de puissances successives en partant de un: 121 = 1 + 3² + 3^3 + 3^4 n² = 1 + p² + p^3 + p^4 Somme de puissances distinctes 23 est le plus grand entier non décomposable en sommes de puissances distinctes Démonstration en utilisant le théorème de Richert. Exemples 22 = 1 + 4 + 8 + 9 23 = IMPOSSIBLE 24 = 8 + 16 25 = 25, etc. Puissances de 3 3^0 = 1 3^2 = 2 + 3 + 4 = 9 3^4 = 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 = 81 3^6 = 14 + 15 + 16 +... + 39 + 40 = 729 etc. avec un nombre de termes égal à: 1, 3, 9 ,27... Équations n = 2 est la seule solution de n^x = n^y + n^z avec 2² = 2^1 + 2^1. a =2 et b= 4, seule solution de a^b = b^a avec 2^4 = 4². Somme des puissances successives La suite des puissances de 2 : 1, 2, 4, 8, 16, 32, 64, 128, 256 ... peut s'exprimer par la fonction : Il se trouve qu'on peut en donner une expression globale, à condition que x < 1, pour que la suite converge : B(x) = 1 / (1 - 2x) Voyons avec x = 0,1: Expression globale Série de puissances B(x) = 1 + 2 x 0,1 + 4 x 0,01 + 8 x 0,001 + 16 x 0,0001 + ... = 1 + 0,2 + 0,004 + 0,008 + 0,0016 +... = 1, 2496 + ... = 1,25 Généralisation: formule célèbre

SOMME DE FACTORIELLES
Seuls deux nombres sont égaux à la somme des factorielles de leurs chiffres: 145 & 40 585. Problème de Brocard Solutions de n! + 1 = x². Il n'en existe que 3. 4! + 1 = 5² = 25 5! + 1 = 11² = 121 7! + 1 = 71² = 5 041

PRODUITS DE PUISSANCES

x^x . y^y = z^z est vérifiée pour:

x = 12⁶ = 2¹² x 3⁶ = 2 985 984

y = 6⁸ = 2⁸ x 3⁸ =

z = 2²⁰ x 3¹⁴ =

x^x = 0,34 10⁹⁷

y^y = 0,17 10⁹⁰

z^z = 0,73 10¹⁰²

1940 - Chao-Ko, Chine 

x^x y^y = z^z

est vérifiée pour :

x = 12^6	= 2^12 x 3^6
y = 6^8	= 2^8 x 3^8
z = 2^11 x 3^7	= 2^11 x 3^7

(1940 - Chao-Ko, Chine)

Suite	1 à 100 en 4 carrés Sommes de cubes et autres puissances  S'y retrouver – Index
Voir	Bi, tripartitions Calcul mental Carré des triangulaires = somme de cubes Conway Cubes Géométrie Nombre = sommes de cubes Nombre = sommes de puissances Nombres carrés Nombres cubes Nombres polygones Nombres triangles Somme des inverses Somme multi puissantes Théorème de Richert Théorie des nombres Unité des puissances
Site	Computing Minimal Equal Sums Of Like Powers – Euler net Autres sites
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThWaring.htm