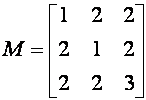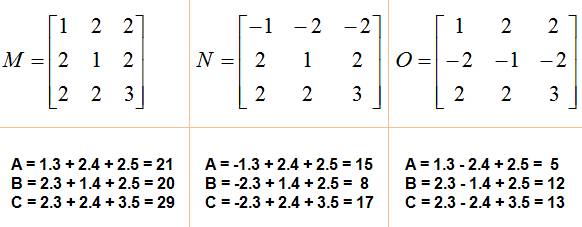triplets de Pythagore

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/10/2020 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Puissances
Débutants Logarithmes	Triplets de Pythagore				Glossaire Puissances
Rubrique PARTITION INDEX PUISSANCES	Introduction	Propriétés	Cercle	Historique
	Primitif	Génération	Matrice	Spéciaux
	Illustration	Triangles	Briques	Calculs
	Avec un carré			TABLES
	Sommaire de cette page >>> Approche >>> Les trois matrices >>> Pyramide des triplets primitifs >>> Théorie

TRIPLETS de PYTHAGORE

Matrices génératrices

Formation de tous les triplets primitifs

APPROCHE

Une formule magique

À partir d'un triplet connu, il est possible d'en former une infinité en utilisant la formule indiquée.

A = a + 2b + 2c

B = 2a + b + 2c

C = 2a + 2b + 3c

Exemples

119

697

4 059

23 661

120

696

4 060

23 660

169

985

5 741

33 461

A²

441

14 161

485 809

16 475 481

559 842 921

B²

400

14 400

484 416

16 483 600

559 795 600

C²

841

28 561

970 225

32 959 081

1 119 638 521

Empreinte

L'empreinte de la formule,

en omettant les variables

est appelée matrice.

Elle est matérialisée par un crochet.

Pour être exact, il faut inverser ligne et colonne.

Ici, elles sont symétriques et cela ne change rien.

Nouvelle écriture

Par convention, la formule s'écrit simplement de la manière suivante.

(A, B, C) = (a, b, c) M

LES TROIS MATRICES

Matrices

Il existe trois matrices génératrices

Exemples

Avec 3 4 5 =>

Notez l'ordre des opérations

Propriétés

Primitifs

Théorème de Roberts (1977)

Si (a, b, c) est un triplet primitif

(a, b, c) M (a, b, c) N (a, b, c) O

sont aussi des triplets primitifs

(a, b, c) est un triplet primitif

si et seulement si

(a, b, c) = (3, 4, 5) L

La matrice L étant le produit fini des matrices M, N et O

Voir Matrices

PYRAMIDE DES TRIPLETS PRIMITIFS

Généralisation

Chaque matrice L, M ou N permet de créer des triplets primitifs en nombre infini.

Le théorème de Roberts permet conjuguer ces matrices et d'engendrer une infinité de combinaisons.

En partant du triplet de départ 3, 4 et 5, il est possible de construire la pyramide infinie de tous les triplets primitifs.

Voici les 4 premiers étages.

3 4 5	21 20 29	119 120 169	697 696 985
			217 456 505
			459 220 509
		39 80 89	377 336 505
			57 176 185
			299 180 349
		77 36 85	319 360 481
			175 288 337
			165 52 173
	5 12 13	55 48 73	297 304 425
			105 208 233
			187 84 205
		7 24 25	105 88 137
			9 40 41
			91 60 109
		45 28 53	207 224 305
			95 168 193
			117 44 125
	15 8 17	65 72 97	403 396 565
			115 252 277
			273 136 305
		33 56 65	275 252 373
			51 140 149
			209 120 241
		35 12 37	133 156 205
			85 132 157
			63 6 65

THÉORIE

Vérification des formules données

Reprenons l'une des formules.

A = a + 2b + 2c

B = 2a + b + 2c

C = 2a + 2b + 3c

Développons la côté gauche de l'égalité de Pythagore.

Le coefficient 5 n'est pas bien sympathique.

A² + B²

= 5a² +8ab +12ac + 12bc + 5b² + 8c²

Astuce pour se ramener à 4: retirer a² et b².

Or, le triplet de départ s'écrit:

retirez a² + b² OK,

mais il faut ajouter une quantité équivalente pour garder l'équilibre

cette quantité c'est c².

a² + b² = c²

- a² - b² + c² = 0

Voyons ce que cela donne =>

A² + B²

= 5a² +8ab +12ac + 12bc + 5b² + 8c²

- a² - b² + c²

= 4a² +8ab +12ac + 12bc + 4b² + 9c²

Sympathique, il y a du 4 et du 9 en coefficients des carrés.

Factorisation possible dans l'air.

En effet =>

A² + B² = (2a + 2b + 3c)² = C²

Les deux autres formules ne sont que des variantes de signes.

Suite	Triplets spéciaux
Voir	Addition - Glossaire Années Pythagore Décade de Pythagore Pythagore - Biographie
Site	Pythagorean Triple de Eric Weisstein
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/TripMatr.htm