|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
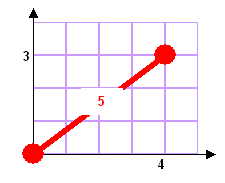
TRIPLETS de PYTHAGORE Illustration
|
|
|
|
|
25 24 25 26 30 23 22 21 29 20 25 29 19 18 30 17 16 20 15 17 25 14 13 12 13 15 20 11 10 26 9 15 8 10 17 7 25 6 10 5 13 4 5 3 5 2 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
|
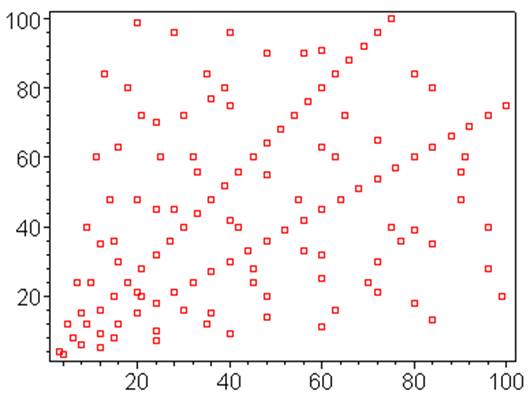
Exemple: 12²
(abscisse)
+ 5² (ordonnée) = 13² (valeur indiquée à l'intersection). On
retrouve, bien sûr, chaque triplet et son symétrique. On observe la ligne
oblique 5, 10, 15 … des triplets
multiples du premier (et la ligne
symétrique par rapport à la diagonale). |
|
|
Axes
|
|
||||||||||||||||||||||||||||||
|
Formule
|
Valeur
de la ligne(L) au carré plus valeur de la colonne (C) donne le carré de
l'hypoténuse (H) L² + C² = H² H = RACINE (L² + C²) Inscrire
H que si sa valeur est entière |
||||||||||||||||||||||||||||||
|
Cellule de départ
Calcul de H
H entier ?
|
H = RACINE(A100*A100+B101*B101) H = RACINE($A100*$A100+B$101*B$101) RACINE($A100*$A100+B$101*B$101)
- TRONQUE (RACINE($A100*$A100+B$101*B$101)
) = 0 ? |
|
Programmation
Tapez
"espace" entre les deux guillemets
SI(RACINE($A100*$A100+B$101*B$101) - TRONQUE
(RACINE($A100*$A100+B$101*B$101)) = 0;RACINE($A100*$A100+B$101*B$101); "
")
|
|
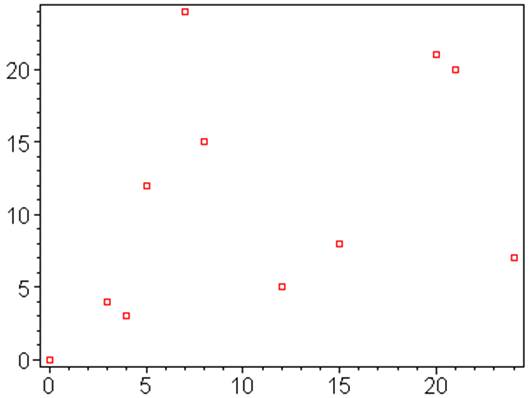
Primitifs sur cette
colonne |
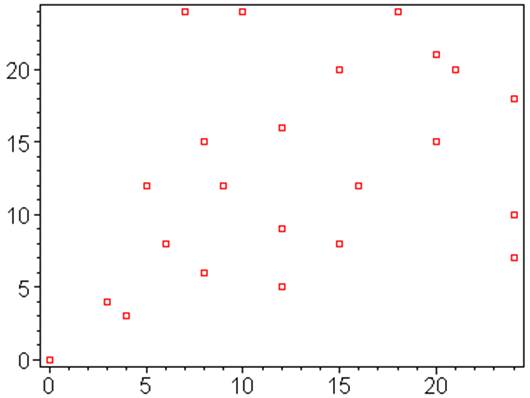
Tous sur cette
colonne |
|
Quantité de points:
2 x 6 |
2 x 11 |
|
2 x 18 |
2 x 63 |
|
2 x 179 |
2 x 1034 |
|
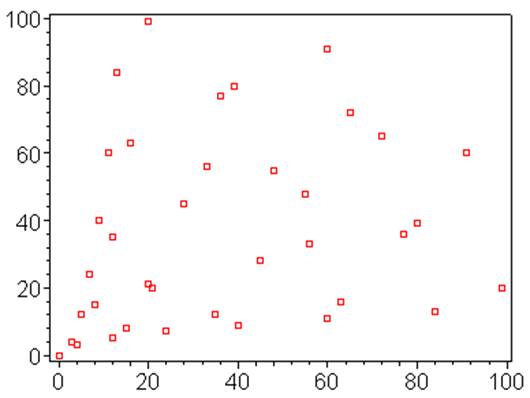
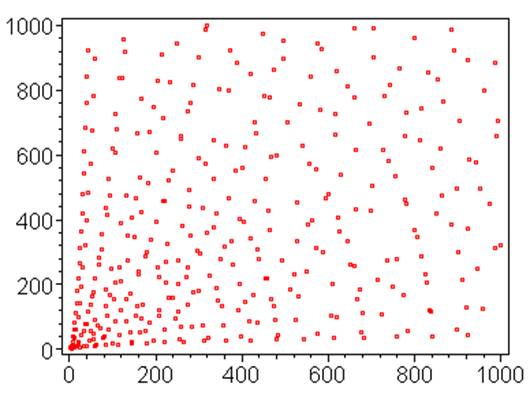
Il n'est pas
étonnant de voir une tendance à former des cercles
(ellipses) dont l'équation est x² + y² = R. |
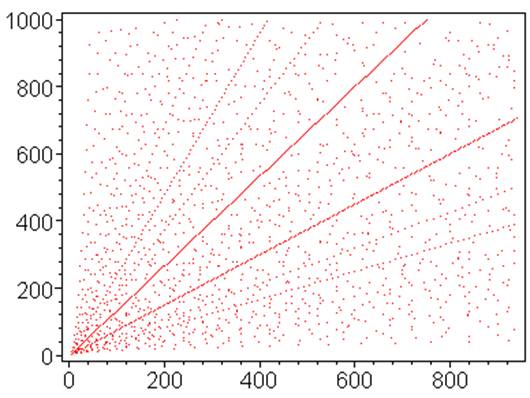
Il n'est pas
étonnant de voir apparaître des droites Ce sont les
multiples des triplets primitifs. |
|
Principe
|
|
||||||||||
|
Programme Initialisation
Mise à zéro des mémoires
Recherche des triplets
Dessin
Décompte
|
#triplets primitifs kt:= 0: mx:= 100: X:= array(1..mx): Y:= array(1..mx): for i from 1 to mx do X[i]:=0: od: for j from 1 to mx do Y[i]:=0: od: k:=1: for i from 1 to mx do for j from 1 to mx do if gcd(i,j)=1 then
h:=sqrt(i*i+j*j):
if h - trunc(h) = 0 then
X[k]:= i:
Y[k]:= j:
k:=k+1:
kt:=kt+1:
fi: fi:od:od: points:= { seq([X[i],Y[i]],i=1..k) }: pointplot(points, axes=BOXED,
color=red, symbol=box): kt; |
![]()
|
Voir |
|
|
Site |
|
|
Cette page |
|
![]()