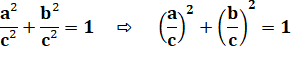|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
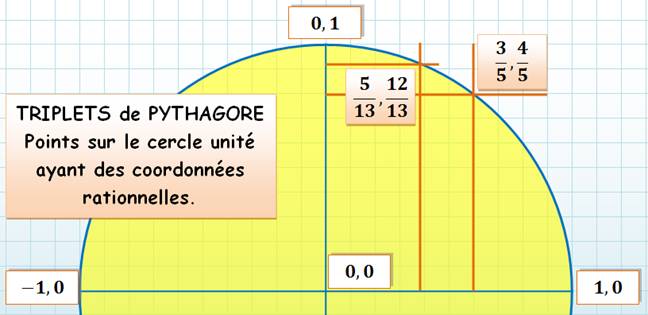
TRIPLETS de PYTHAGORE Cercle Unité
|
|
|
|
|
|
|
|
|
|
|
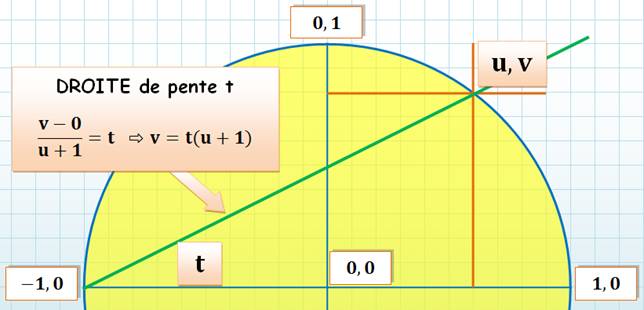
nous pouvons choisir les coordonnées (u, v) en
fonction de t:
Ces valeurs, exploitant une identité remarquable, remplissent les conditions requises: u² + v² = 1 En effet: 1
– 2t² + t4 + 4t² = 1 + 2t² + t4 = (1 +t²)² Et v = t(u
+ 1) 2t = t (1 – t²)
+ (1 + t²) 2t = t – t3
+ t + t3 = 2t vérification terminée. Le choix de ces valeurs semble parachuté; en fait,
il résulte d'une intuition aidée par une bonne connaissance des identités
remarquables.
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/TripCerc.htm |
![]()