|
|||||||||||||||||||||||||||||||||||||||||||
![]()
|
CARRÉS MAGIQUES à contraintes Ou carré magique à trous. Il s'agit de compléter le carré magique. |
|
|
||
|
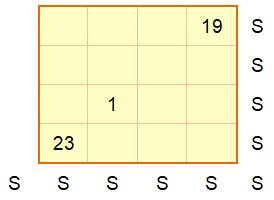
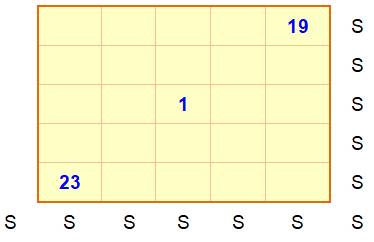
Résoudre ce carré magique d'ordre 4. S est la somme magique à obtenir sur
les lignes, les colonnes et les diagonales. |
|
|
|
|
|||||||||||||||||||||||||||||||
|
Est-ce carré magique normal? Non! Pour un carré magique normal d'ordre
4, on utilise les nombres de 1 à 16. Visiblement ce carré n'est pas normal,
puisque nous rencontrons 19 et 23. Quelle est la somme magique? Nous voyons 23 dans le tableau. Avec un tel carré, on peut utiliser des
nombres parmi 1 à 23 au moins Aucune contrainte n'est donnée Par conséquent, la somme n'est pas
déterminée. Valeur minimale des nombres
utilisés Du fait de la présence du 1 la valeur
minimale des autres nombres est 2 Peut-on compléter certaines
cases ? Oui, la somme sur les diagonales donne la
somme magique S = 23 + 1 + x + 19 et x = S – 43
Valeur minimale de la somme La valeur minimale de x est 2 x min = 2 S min = 43 + 2 = 45 Valeur maximale des nombres Elle est obtenue dans le cas ou les trois
autres nombres d'une somme sont minimaux. Toutes autres valeurs feraient
diminuer la valeur de xmax. S = 1 + 2 + 3 + x max x max = S – 6 |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Quels sont les paramètres
d'exploration? Avec les considérations précédentes, on
peut chercher les carrés dont la somme est S = 45 ou plus avec des chiffres parmi 1 à x max = 41 ou plus Les premières solutions apparaissent pour S = 49, et il y en a 5:
Solutions pour S
= 50, il y en a 2 seulement:
Évidemment cela continue pour S > 50. Donc, de très nombreuses solutions. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||
|
|
|
|
|
Procédé par analogie |
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
Merci à Pierre
L. pour
sa contribution
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMContra.htm |
![]()