NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/01/2020 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Bases et amusements				Glossaire Carrés magiques
INDEX Carrés magiques Jeux numériques	Latin	Gréco-latin	Avec 0 à 9	Vers Magiques
	Jeux (à trous)	Échelle alternée	Décimal	Sudoku
		Cartes à jouer
		Sommaire de cette page >>> Approche >>> Ordre 3 – Deux fois latin >>> Définition et construction à partir de carrés latins >>> Ordre 4 – Les cartes d'Ozanam >>> Ordre 5 et 7 – Exemples >>> Ordre impair construction >>> Ordre 6 – Les 36 officiers d'Euler >>> Historique >>> Ordre 6 en 3D – Le jeu des 36 cubes >>> Ordre 8 >>> Ordres supérieurs: 9 et 10 >>> Bilan

Carrés GRÉCO-LATINS

ou Eulériens

Jeux de grille carrée tels chaque ligne, comme chaque colonne, comporte des deux symboles (dessins, chiffres …) tous différents.

Euler, les étudia en détail. Il nota le premier jeu de symboles avec des lettres latines et le second jeu avec les lettres grecques. D'où le nom de carré gréco-latin. Il avait conjecturé que de tels carrés n'existaient pas pour n = 4k + 2; prouvé fausse seulement récemment. On désormais qu'ils existent pour tout n sauf 6.

Les carrés gréco-latins, au-delà du divertissement, sont utiles pour composer des équipes lors de tournois. Ils sont utilisés pour construire des carrés magiques.

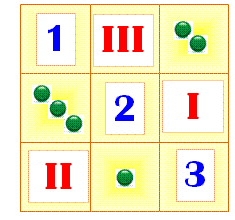
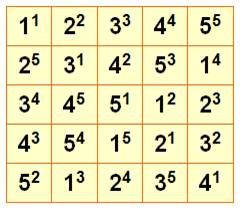
Carré formé avec des nombres entiers, des chiffres romains et des points de dés

APPROCHE
Formes et couleurs: exemple de carré gréco-romain Un tableau de quatre lignes et quatre colonnes. Seize motifs avec quatre dessins et quatre couleurs. Placez les motifs tels qu'ils soient différents sur les lignes, comme sur les colonnes.	Un seul cercle apparait dans ligne et dans chaque colonne. Le jaune est présent dans une seule ligne et une seule colonne. Le rond jaune n'est présent qu'une seule fois.

DEUX FOIS LATINS

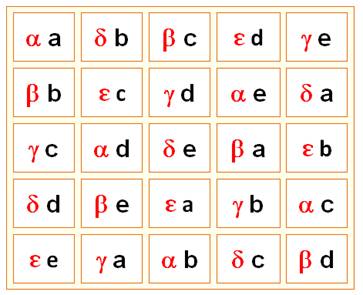
Le carré latin est un cousin du carré magique. C'est un carré ayant pour éléments les entiers 1, 2,..., n ou toute suite de n nombres distincts, chacun de ces nombres figurant n fois et étant placés de telle sorte que les entiers de toute ligne ou de toute colonne soient distincts.

En voici deux distincts:

Superposons le second au premier, en conservant le même ordre, pour former le carré des paires.

Aucune paire n'est répétée.

Un tel carré de paires, sans répétition de paires, est appelé carré eulérien, en référence au mathématicien suisse Leonhard Euler, ou carré gréco-latin.

Les carrés latins et eulériens ont suscité un intérêt considérable.

Une fois latin

1	2	3	1	2	3
2	3	1	3	1	2
3	1	2	2	3	1

Deux fois latins

1 , 1	2 , 2	3 , 3
2 , 3	3 , 1	1 , 2
3 , 2	1 , 3	2 , 1

Définition et construction
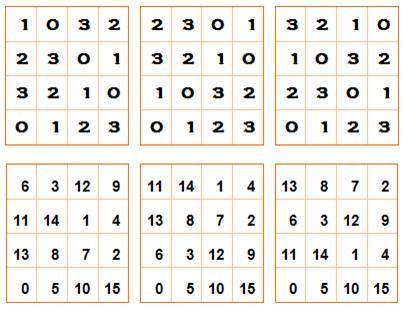
Carré gréco-latin Carré eulérien Carré bilatin Carrés latins orthogonaux Tableau n par n de n couples de motifs, répartis de manière les motifs ne se retrouvent qu'une seule fois dans chaque ligne et chaque colonne. Il y aura n² couples. Construction avec deux carrés latins croisés Chacun des deux jeux de symboles constitue un carré latin particulier (illustration en haut). Le carré latin de gauche présente une symétrie centrale. Celui de droite montre la même suite de lettre en ligne du haut a b c d. Même succession sur les lignes suivantes en inversant le sens et en décalant. Leur combinaison produit un carré gréco-latin.	Ordre 4 avec lettres Ordre 4 avec nombres
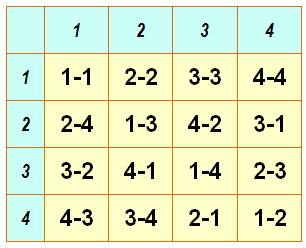
Un autre exemple d'ordre 4 et sa construction Le premier carré latin est diagonal (chacun des chiffres sur les deux diagonales). Chaque ligne est une copie par permutation circulaire sur les lignes 1, 4, 2 puis 3. Le second carré est obtenu de la façon suivante: première ligne identique; deuxième ligne par permutation deux à deux; troisième ligne par permutation par bloc de deux; et quatrième ligne par permutation double. En superposant les deux, on obtient un carré gréco-latin. Propriété essentielle: il est magique, ce qui est assez logique compte-tenu de sa méthode de construction. Cette propriété est exploitée pour construire un carré magique classique (avec les nombres de 1 à 16) >>>

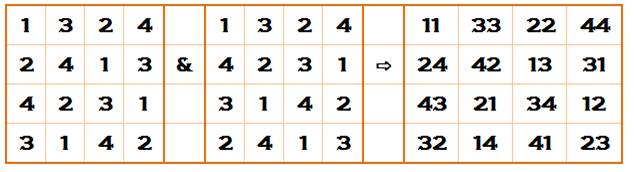
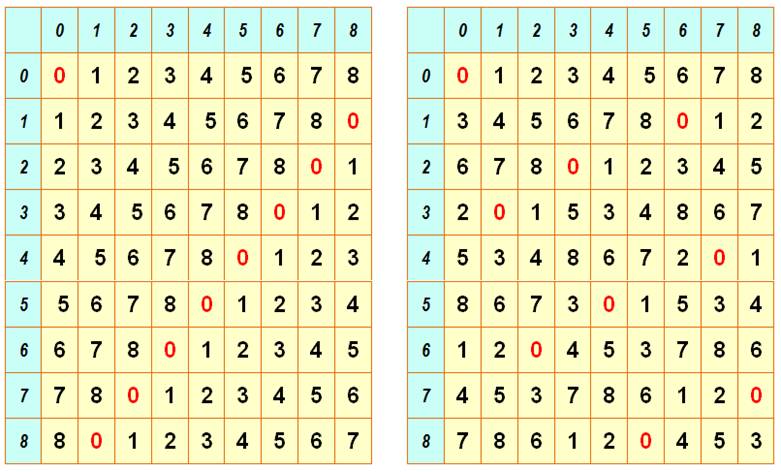
Exemple de trois carrés latins mutuellement orthogonaux (MOLS)

Les carrés du bas composent ceux du haut deux par deux en passant de la base 4 en base 10. Exemples: 1 x 4 + 2 = 6; 0 x 4 + 3 = 3; 3 x 4 + 4 = 12; etc.

Les valeurs du bas étant toutes différentes sur chaque carré, les carrés du haut sont orthogonaux. Notez que les carrés du bas sont semi-magiques. Pour obtenir la somme magique sur les diagonales, il aurait fallu que celles-ci contiennent les nombres de 0 à 3 une seule fois.

Ordre 4 – Les cartes d'Ozanam

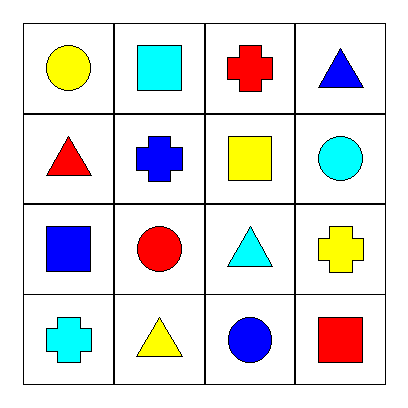
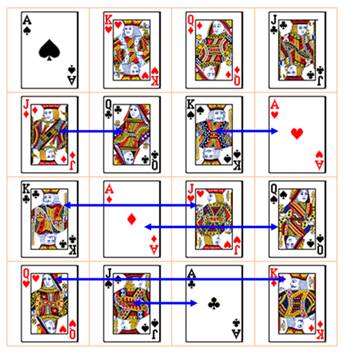
Problème Les as, rois, dames et valets d'un jeu de cartes. Disposer ces cartes sur une grille 4 x 4 de façon que chaque ligne et chaque colonne montre une carte de chaque valeur et une carte de chaque couleur (on dit aussi: enseigne). En plus, la même contrainte est appliquée aux deux diagonales principales. En 1725, Jacques Ozanam (Récréations mathématiques et physiques) pose ce problème. Solution Martin Gardner indique que c'est Kathleen Ollerenshaw qui trouva la quantité correcte de solutions: 144 qui avec les huit réflexions et rotations conduit à 1152 solutions. Cependant, du fait des permutations, elles peuvent se résumer à ces deux types: Disposition pour le carré de gauche Premier type Deuxième type Les flèches bleues montrent comment passer du premier type au second.

Exemples n = 5 et n = 7
N = 5 (ordre 5)	N = 7 (ordre 7) N = 5 (ordre 5) Avec notation préférée d'Euler

Voir Carrés latins orthogonaux d'ordre impair – Construction

Ordre 6 – Les 36 Officiers (ou grenadiers) d'Euler
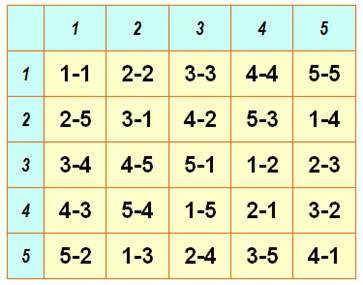
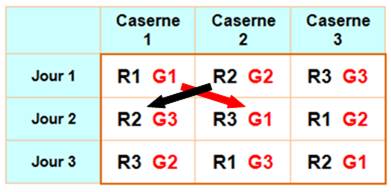
Problème posé par Euler en 1779 36 Officiers, 6 régiments, 6 grades. Un tableau 6x6. Chaque ligne doit contenir chacun des grades et chacun des régiments. On reconnait que les deux carrés latins sous-jacents sont orthogonaux et leur construction (flèches)	Exemple avec un tableau 3 x 3 Un régiment et un grade différent pour chaque caserne et chaque jour Prolonger avec 4x4 ou 5x5, c'est possible; avec 6x6, c'est impossible: 1782 – constat par Euler. 1901 – démonstration par Gaston Tarry Voir Historique Le cas de quatre officiers à repartir dans une grille de 2x2 est également impossible.

Voir 36 dans un fortin / Euler et la construction des carrés magiques

Le jeu des 36 cubes

Ce jeu est très proche du problème des officiers d'Euler. Il s'agit de composer un carré gréco-latin de 6 x 6 en empilant des tiges creuses de six couleurs et six longueurs. Normalement, c'est impossible. Le jeu comporte une subtilité sur deux tiges qui rend la formation du carré possible. Deux tiges sont interchangeables sans modifier la longueur totale. Il existe 96 solutions pour une bagatelle de 6!^6 =139 314 069 504 000 000 combinaisons. Jeu conçu par Derrick Niederman (alors qu'il écrivait un livre sur les nombres entiers) et construit par ThinkFun.

Ordre 8

Ordres supérieurs
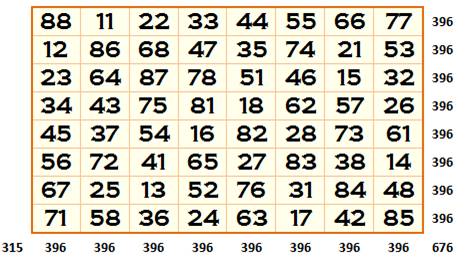
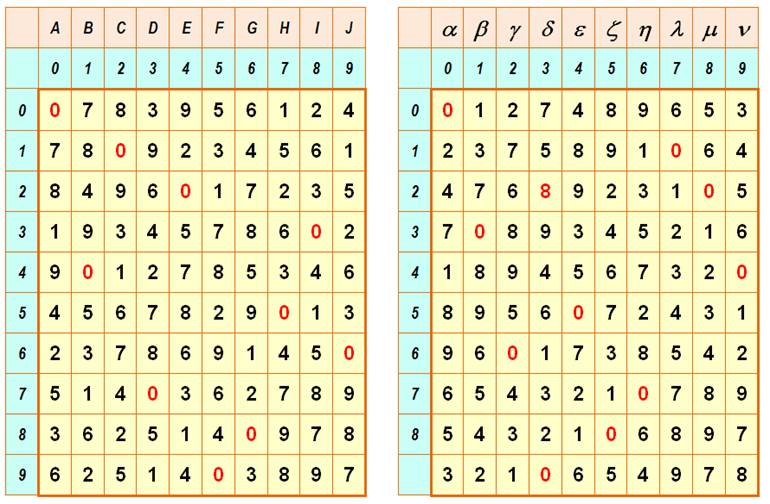
Sauf coup de chance, il est quasiment impossible de trouver de tels carrés sans ordinateur. (You are unlikely to find one just by using trial-and-error without a computer). Ordre 9 Ordre 10 Les lettres en haut pour ceux qui voudraient recréer le carré gréco-latin dans son acception originale

Bilan

La notion de carrés latins orthogonaux peut être étendue à plus de deux carrés.

Elle peut également être généralisée avec la présence de k fois chaque élément sur chaque ligne ou colonne. Deux tels carrés sont orthogonaux si, superposés, chaque couple apparait k² fois.

Anglais

A Latin square arrangement is an arrangement of s symbols in s rows and s columns, such that every symbol occurs once in each row and each column. When two Latin squares of same order superimposed on one another, then in the resultant array every ordered pair of symbols occurs exactly once, then the two Latin squares are said to be orthogonal.

A famous conjecture of Leonhard Euler on orthogonal Latin squares had recently been proven false after more than 100 years of valiant effort.

In 1900, G. Tarry has proven that no orthogonal squares of order 6 exists thus lending credibility to the Euler's conjecture. In 1960, it was shown by Bose, Shrikhande, and Parker that, except for this one case, the conjecture was false.

MOLS: mutually Orthogonal Latin Squares

Voir Anglais

Suite	Carrés gréco-latins – Théorie, propriétés, quantité Carré latins avec les chiffres de 0 à 9 Carrés gréco-latins à échelle alternée (vers Franklin) Carrés magiques et jeux Sudoku Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Carrés mystérieux Dominos magiques Géométrie Jeux Jeux de chiffres Nombres magiques - Index Pannumérique Rubriques débutants
DicoNombre	Nombre 36
Sites	L'histoire des trente-six officier – Mathkang Greco-Latin Squares ans a Mistaken Conjecture of Euler – Dominique Klyve and Lee Stemkoski – 2003
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMgreco.htm