|
||||||||||||||||||||||||||||||||
![]()
|
FIGURES
MAGIQUES Croix,
triangles, carrés, polygones, étoiles, etc. |
|
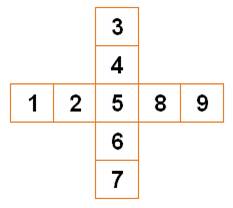
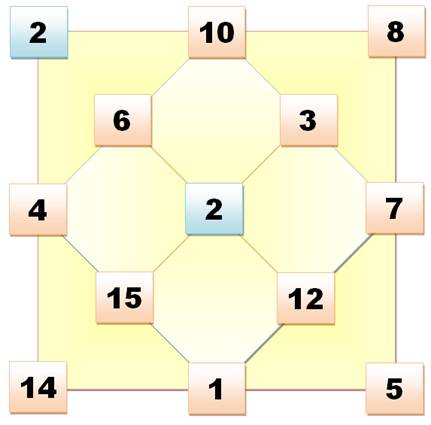
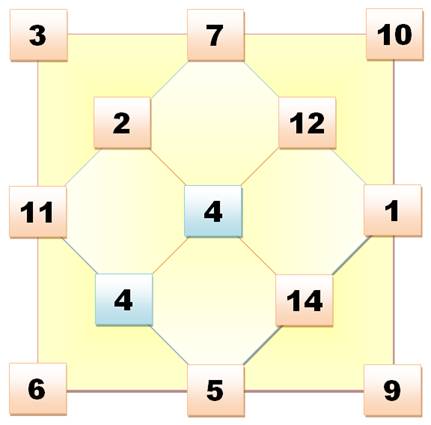
Sur
ces quatre croix, aucun des nombres de 1 à 8 ne côtoient un de ses voisins
numériques en horizontal, vertical et diagonales. La configuration du bas est
identique à que celle du haut par symétrie.
Au centre, les deux
nombres extrêmes 1 et 8 qui positionnent le 2 et le 7. Les nombres suivants
se positionnent automatiquement. |
Voir Pannumériques
|
|
|
|
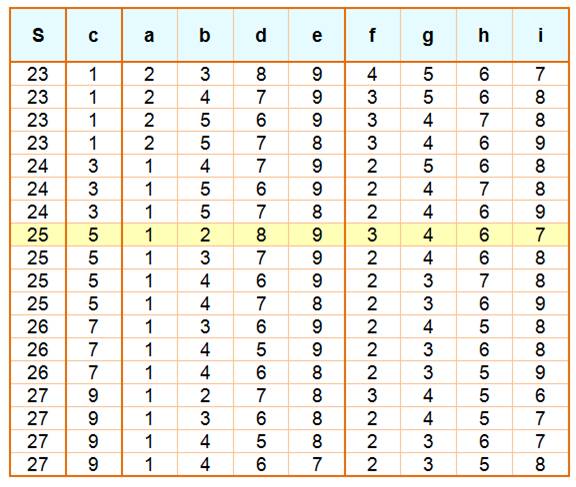
Somme verticale
et somme horizontale égales. La croix comporte 9 chiffres différents. Celui
du centre est commun aux deux sommes. Exemple
Les
deux sommes valent 25. Les 18 possibilités
(hors permutations et rotations) L'exemple
ci-dessus est marqué en jaune dans le tableau S
= somme et c est le chiffe central
|
|
|
|
Voir Énigmes
– Index
|
|
|||||
|
Ordinaire
|
|||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Exemple de lecture: 1 + 6 + 2 = 2 + 4 +
3 = 3 + 5 + 1 = 9 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
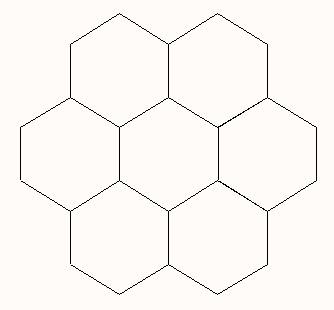
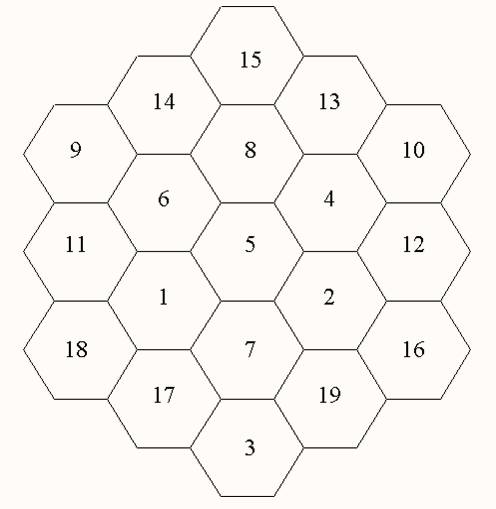
Illustration du modèle le
plus simple :
Hexagone magique le plus
petit :
Autres hexagones
magiques :
|
|
Voir Autres hexagones magiques (autre type) / Hexagone
mystérieux
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Cercle japonais (1660)
Cercle de Yang Hui (1275)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Cercles
à circonférence magique
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Livre |
|
|
Sites |
|
|
Cette page |
![]()
Renvois de
liens
Suite - Figures magiques