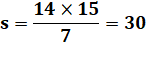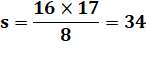|
||||||||||||||||||||||||||||
![]()
|
ÉTOILES MAGIQUES Étoile magique de David ou à six
branches Somme constante sur les
branches des étoiles à k branches. Le cas
de k = 6 (hexagramme ou étoile de
David) est étudié plus en détail sur ces pages. La recherche concernant les étoiles magiques a soulevé autant
d'enthousiasme que la recherche des carrés magiques: Dudeney, Gardner,
Hendricks, Leeds, Mutsumi Suzuki … et, plus récemment, Harvey Heinz qui a
constitué une véritable référence sur ses pages. |
|
|
|||
|
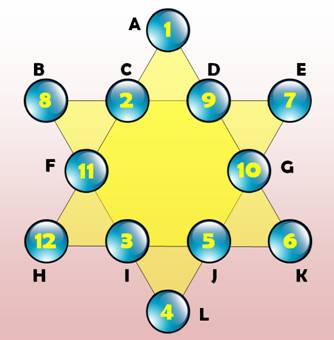
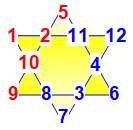
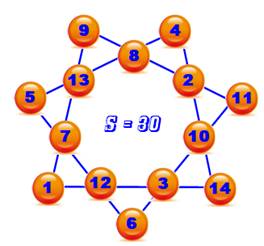
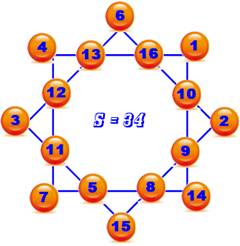
Étoile à six branches ou hexagramme ou étoile magique de David Chaque étoile est formée avec 12 nombres, dont 6 sont les sommets et 6
les creux. Chacun des nombres participe à la somme sur deux branches différentes. Notez la position du nombre 1 soit en sommet soit en
creux. |
|
||
|
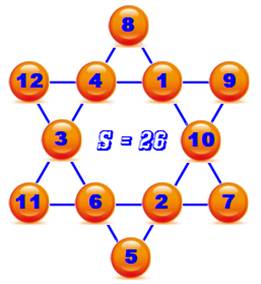
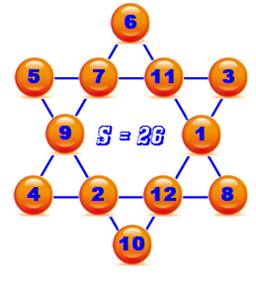
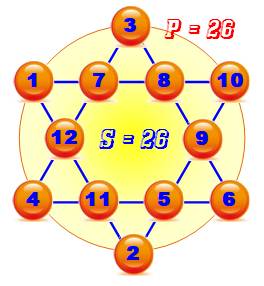
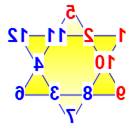
La somme
est bien constante sur chacune des branches. En plus,
la même somme se trouve sur la périphérie (exemple)
ou sur les creux. |
|
||
Voir Transformation de l'étoile magique en cubes magiques
|
|
|||||||
|
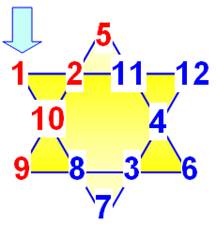
L'étoile
à six branches comporte douze emplacements pour les nombres de 1 à 12, dont
la somme
vaut T. |
T = 1 + 2 + 3 + … + 12 = 12 x 13 / 2 = 78 |
||||||
|
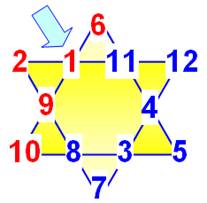
Chaque
nombre est impliqué deux fois dans une des six sommes. Le total
des nombres de 1 à 12 vaut deux fois la somme des nombres sur les six
branches, et c'est aussi six fois la somme magique s. |
6s = 2T = 12 x 13 s = 2 x 13 = 26 |
||||||
|
Les 33 partitions primitives du nombre 26 avec quatre nombres différents parmi les nombres de 1 à
12. Avec les 24 permutations possibles de chacune, il
y a 792 partitions. |
|
||||||
|
Symétries et rotations Avec six axes de symétrie et six rotations possibles, une étoile primitive
engendre douze étoiles semblables. |
|
||||||
|
Étoiles primitives Seule importe la position du nombre 1 au
sommet ou en creux. Toutes les autres configurations s'en déduisent par rotations et
symétries. |
Type 1
|
Type 2
|
|||||
|
Dénombrement Les 80 étoiles primitives à six branches dont 12 diaboliques Les 80 forment quatre familles de 20 super-primitives |
Suite
en Page dédiée |
||||||
Voir Étoile
à six branches – Géométrie
|
Heptagramme
Octagramme
|
|
Voir Polygones
![]()
|
|
||
|
Avec logiciel Le dénombrement est immédiat
avec un logiciel mathématique
(Maple). Programme
Voir Programmation – Index
|
Commentaires Le programme calcule toutes les partitions
de 26 avec les nombres de 1 à 12, puis, avec une boucle, il trie celles qui
comptent quatre termes différents. Chaque partition retenue est ajoutée à la
liste Part4. Résultat Il y a 2063 partitions du nombre 26 avec
les nombres de 1 à 12 et seulement 33 avec quatre termes différents. |
|
|
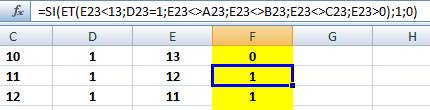
Avec tableur Il est
facile de réaliser le dénombrement avec un tableur. Développer
123 = 1728 lignes énumérant les valeurs de a, b et c de 1 à 12
pour chacun. Créer une
colonne avec 1 si les trois nombres sont différents.
Sur la
colonne suivante (E), on calcule la différence: d = 26 – a – b – c. Créer une
nouvelle colonne conditionnelle qui vérifie que d est compris entre 1 et 12
et qu'il est différent de a, b, et c.
En fin de
table, demander la somme de la colonne F et divisez par 24:
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMgeomEt.htm |
![]()