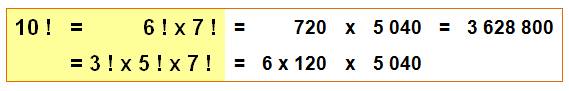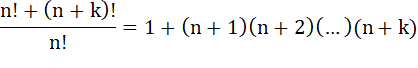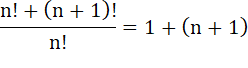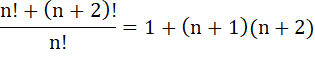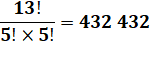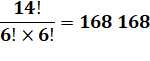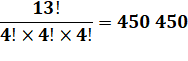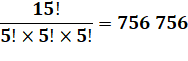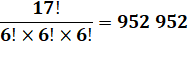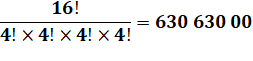|
|||||||||||||||||||||||||||
![]()
|
Produit et quotient de FACTORIELLES Identités
remarquables sur les produits et quotients de factorielles voisines. |
|
|
||
|
Produit On ne connaît que ces cas de la forme indiquée. Progression arithmétique Les trois cas connus: 0! x 1! x 2! = 2! 1! x 3! x 5! = 6! 1! x 3! x 5! x 7! = 10! |
Trivial 0!
x n! = n! 0!
x 1! x n! = n! 1!
x n! = n! Cas à
noter 1!
x 3! x 5! x 7! = 10! 6! x 7! = 10! Suite >>> |
|
|
Somme De même, quatre cas de la forme indiquée. Seuls existants: prouvé. |
1 = 1! 2 = 2! 145
= 1! + 4! + 5! 40
585 = 4! + 0! + 5! + 8! + 5! |
|
Nombres atteint par une division de
factorielles
|
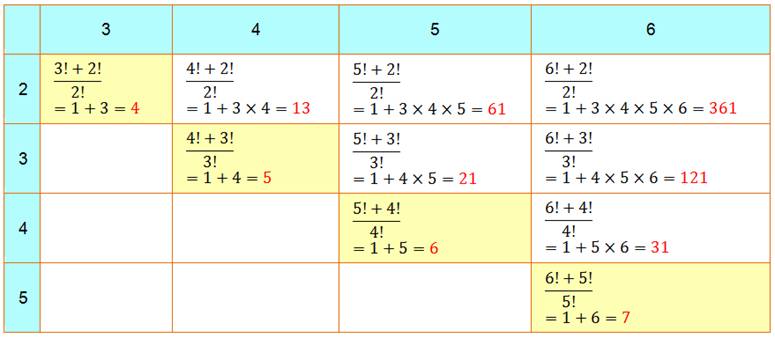
Tout
nombre est exprimable de cette façon:
Sinon quelques
nombres sont exprimables avec ce type de division comme (voir
tableau):
|
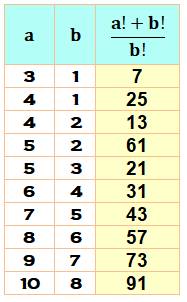
Notez la présence de 13 et 31 |
|
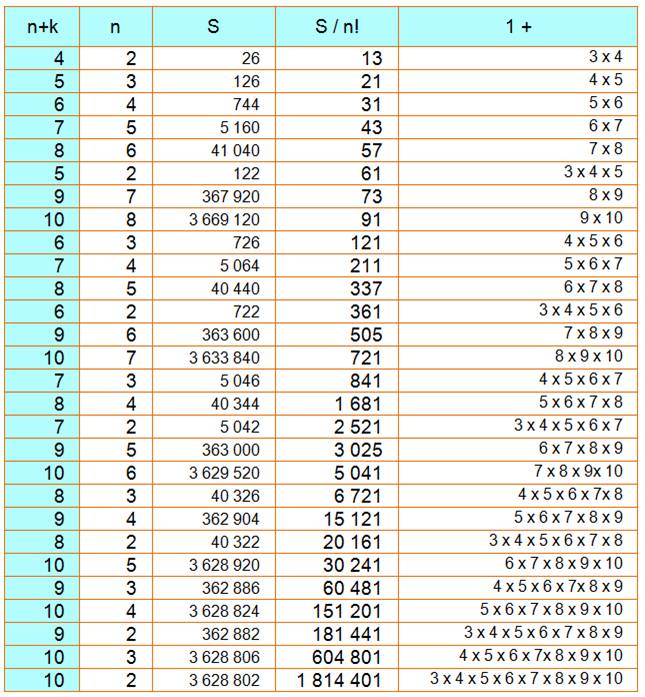
Nombres exprimables
par cette sorte de division de factorielle juqu'à 1000 [a, b,
Fraction] [3, 1, 7], [4, 1, 25], [4, 2, 13], [5, 1, 121], [5, 2, 61],
[5, 3, 21], [6, 1, 721], [6, 2, 361], [6, 3, 121], [6, 4, 31], [7, 3, 841], [7, 4, 211], [7, 5, 43],
[8, 5, 337], [8, 6, 57], [9, 6, 505], [9, 7, 73], [10, 7, 721], [10, 8, 91],
[11, 8, 991], [11, 9, 111], [12, 10, 133], [13, 11, 157], [14, 12, 183], [15,
13, 211], [16, 14, 241], [17, 15, 273], [18, 16, 307], [19, 17, 343], [20,
18, 381], [21, 19, 421], [22, 20, 463], [23, 21, 507], [24, 22, 553], [25,
23, 601], [26, 24, 651], [27, 25, 703], [28, 26, 757], [29, 27, 813], [30,
28, 871], [31, 29, 931], [32, 30, 993] |
|
Voir Identités
|
|
||
|
Produit de 2 factorielles: - Cas général des nombres eux-mêmes des
factorielles Prenons
le nombre 6 qui est une factorielle 6 = 3! Sa factorielle 6!
= 6 x 5 x 4 … = 6
x 5! Ou encore
6! = 3!
x 5! Cette remarque s'applique à toutes les
factorielles.
- Cas particulier
Seul cas de
factorielle, produit de deux factorielles consécutives. Produit de 3 factorielles
Etc. Produit de 4 factorielles Hors termes en 1! qui sont les cas indiqués ci-dessus
Etc. |
||
|
|
|
|
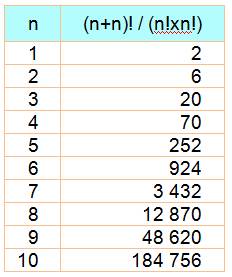
Soit un nombre entier égal à un produit de nombres
consécutifs plus un.
Tableau des
premières valeurs
Notez la
présence de 13 et de son retourné 61. Liste des valeurs
successives
|
|
Voir Jeux
des quatre 4 / Factorielle
divisée
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette
page |
![]()