|
|||||||||||||||||||||||||||
![]()
|
FACTORIELLES Théorème de Wilson Divisibilité des factorielles plus un. Et, quelques curiosités sur les factorielles. |
|
|
|||
|
Propriété Voyons une
propriété plus simple que celle énoncée par le théorème de Wilson. On sait évidemment
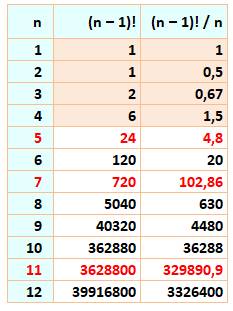
que tous les nombres jusqu'à n divisent le nombre factoriel n. Mais, est-ce
que le nombre n divise la factorielle précédente (n – 1) ! ? Par
exemple, est-ce que 6 divise 5! = 1 x 2 x 3 x 4 x 5 ? La réponse
est toujours oui pour n supérieur à 4, sauf si le nombre n est premier.
|
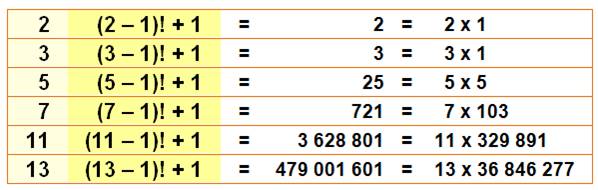
Exemples
|
||
|
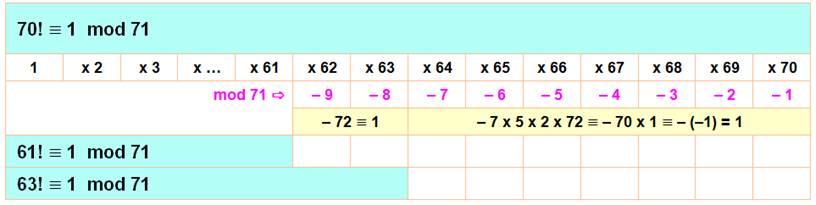
Théorème Si n >
4 est composé alors n
divise (n – 1)! |
|
||
Voir Brève
856
|
|
|||||
|
Théorème
et formulations alternatives
Suitede l'historique >>>
|
|||||
À noter
|
n! + 1 = premier: existence en nombre infini ? n! + 1 = carré: existence en
nombre infini ? |
Voir Des
exemples
|
|
|
|
|
|
|
|
||
|
Deux
factorielles consécutives +1 sont premières entre elles: (n! + 1, (n+1)! + 1) = 1
|
||
|
Elle repose sur la propriété
des PGCD |
(a,b) = ( a, b – ka) |
|
|
Notre expression peut ainsi
s'écrire: |
(n! + 1, (n+1)! + 1) = (n! + 1, (n+1)! + 1 – (n
+ 1) (n! + 1) ) = (n! + 1, (n+1)! + 1 – (n +
1)n! – n – 1) = (n! + 1, (n+1)! + 1 –
(n+1)! – n – 1) = (n! + 1,– n) = 1 |
|
|
Nombres tels que
p² divise (p – 1)! + 1. Les trois seuls
connus: 5, 13 et 563. Le suivant serait >
5 . 108 – K. Dilcher et C. Pomerance |
Voir
Nombre
563 / Nombre
de Wilson / Types de
premiers
|
Vers 1000 – Le mathématicien arabe Alhazen (965-1039) fait référence à
cette propriété dans l'un des ses écrits. vers 1700 – Gottfried Wilhelm Leibniz
(1646-1716) énonce cette propriété, sans la démontrer. 1770 – John Wilson, avec son professeur Edward Waring, redécouvre cette
propriété et la publie en tant que conjecture. 1771 – Joseph-Louis Lagrange est
l'auteur des deux premières démonstrations. 1773 – Leonhard Euler en propose une troisième. Vers 1800 – Carl Friedrich Gauss (1777-1855) reformule la démonstration
d'Euler et en donne une quatrième en utilisant les notations de
l'arithmétique modulaire. |
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()