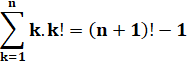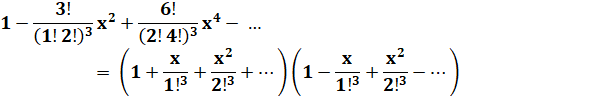|
|||||||||||||||||||||||||||
![]()
|
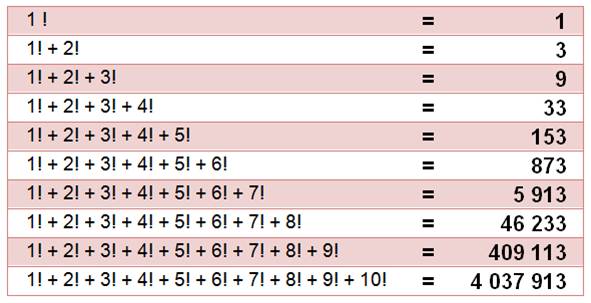
Sommes et Différences de FACTORIELLES Valeur des sommes
cumulées des factorielles. Parfois notée !!n (!!4 = 0! + 1! + 2! + 3! = 10) Somme de
factorielles consécutives ou proches. Possibilité de mise en facteurs et de
mise en évidence de formules simples. |
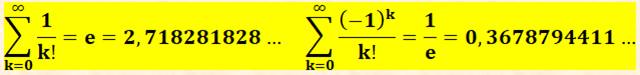
Voir Valeurs
de e (Newton) / Une application: compter
les trajets
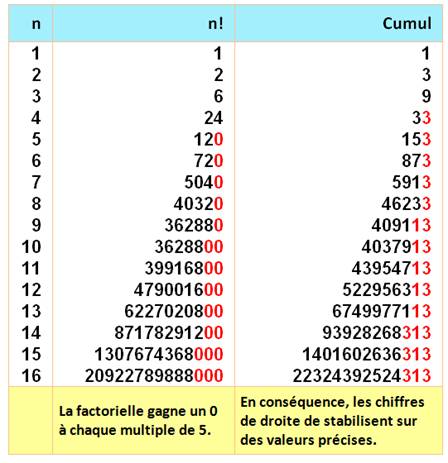
Voir Nombre 13 / Nombre
313 / Nombre
5 913
|
de
factorielles proches |
|
|
|
Identités
avec des factorielles. Que
vaut la somme de deux factorielles consécutives? ou proches? |
||
|
(n
+ 1)! + n! = (n + 1) n! + n! = (n + 2) n! |
2 +
1 = 3 = 3 x 1 6 +
2 = 8 = 4 x 2 24 +
6 = 30 = 5
x 6 120
+ 24 = 144 = 6 x 24 720 +
120 = 840 = 7 x 120 |
|
|
(n
+ 2)! + n! = (n + 2) (n + 1) n! + n! =
(n² + 3n + 3) n! |
6 +
1 = 7 = 7 x 1 24 +
2 = 26 = 13 x 2 120 +
6 = 126 = 21 x 6 720 +
24 = 744 = 31 x 24 5 040 +
120 = 5 160 = 43 x 120 |
|
|
(n
+ 1)! – n! = (n + 1) n! – n! = n. n! |
2 –
1 = 1 6 –
2 = 4 = 2 x 2 24 –
6 = 18 = 3 x 6 120
– 24 = 96 = 4 x 24 720 –
120 = 600 = 5 x 120 |
|
|
(n
+ 2)! – n! = (n + 2) (n + 1) n! – n! =
(n² + 3n + 1) n! |
6 -
1 = 5 = 5 x
1 24 –
2 = 22 = 11 x
2 120 –
6 = 114 = 19 x 6 720 –
24 = 696 = 29 x 24 5 040 –
120 = 4 920 = 41 x 120 |
|
|
Somme
ou différence entre deux factorielles |
(n + k)! + n! = (A +
1) . n! (n + k)! – n! = (A –
1) . n! avec |
|
Voir Identités
|
|
||
|
Relations
Exemple 1x1!
+ 2x2! + 3x3! + 4x4! = 1 + 2x2 + 3x6 + 4x24 = 1 + 4 + 18 + 96 = 119 Or,
(4 + 1)! – 1 = 120 – 1 = 119 Démonstration
Ce
que l'on ajoute sur la ligne 2 est soustrait en ligne 3. Là est l'intuition
astucieuse pour effectuer cette démonstration. Ligne
4 = ligne 2, en calculant n(n – 1)! = n! Ligne
6 = bilan des lignes 4 et 5, en constatant que les termes sur une diagonale
descendante s'annulent. |
||
Formule de Ramanujan produite en 1936 par Hardy
|
|
Source: Le
comptable indien
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()