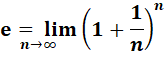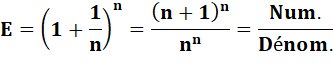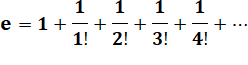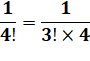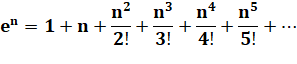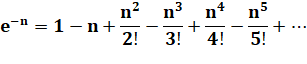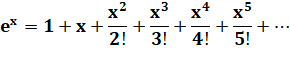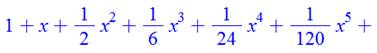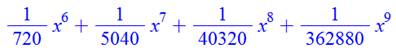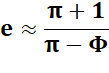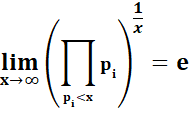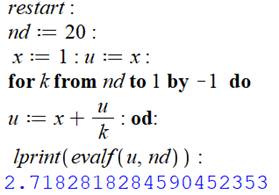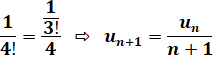|
||||||||||||||||||||||||||||||
![]()
|
"E" en FORMULES Expressions permettant de
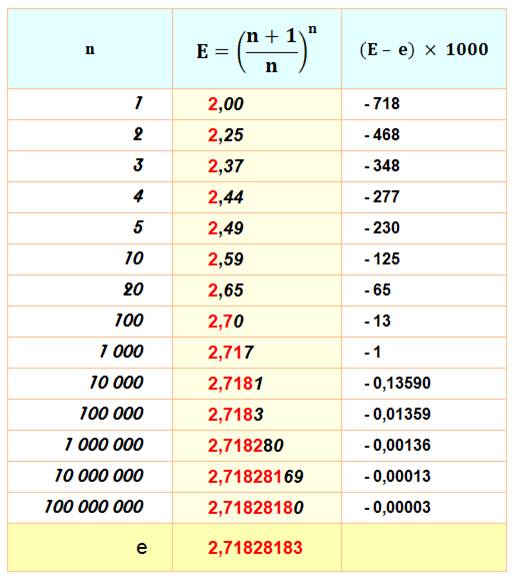
calculer la valeur de la constante "e". Calcul pratique sur calculette |
Voir Pourquoi avoir choisi
e = 2,718
|
Question
|
|
|
Ce n'est pas
possible! |
|
|
Explication |
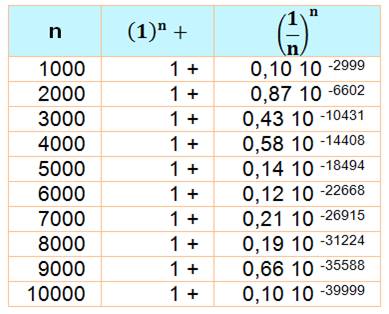
Moralité: La puissance d'une somme n'est pas égale à la somme des
puissances, même à l'infini. |
|
|
||
|
Formule |
|
|
|
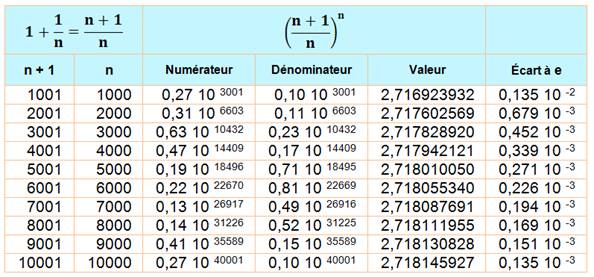
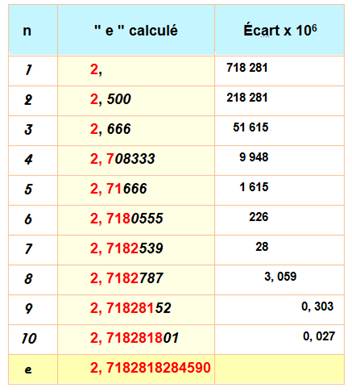
Convergence |
|
|
|
Calcul pratique |
|
|
Voir Factorielles / Sommes / Calcul des
fractions
|
|
||
|
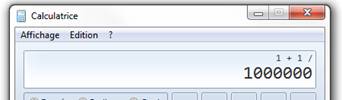
Calcul de e Utilisation de la formule exponentielle avec n = 1 000
000 1) Tapez: 1 +
1/1000000; Cliquez = 2) Cliquez sur
le bouton xy Puis tapez
1000000. Cliquez = L'affichage
donne: E = 2, 718 280 e = 2, 718 281 … Valeur souvent
suffisante pour vos calculs. Calcul d'une puissance de e
Faire appel à
nouveau au bouton puissance xy. |
Cette
calculatrice est celle de votre ordinateur (voir dans le répertoire
accessoire de tous les programmes) |
|
|
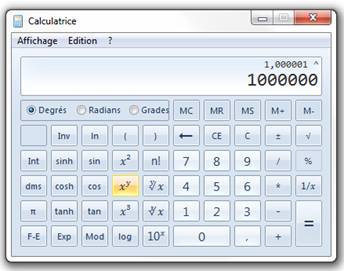
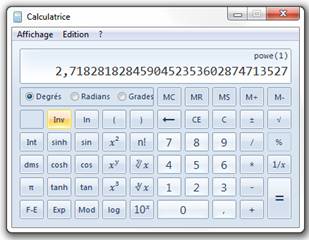
Si la fonction existe C'est immédiat,
bien sûr! Sur cette
calculatrice, on va calculer exp(1). 1) Tapez 1 3) Cliquez sur
le bouton ex; L'affichage est
celui donné ci-contre, avec 32 chiffres |
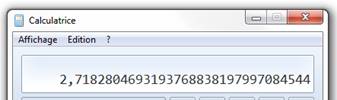
E = 2, 7182818284 5904523536 0287471352 7 e
= 2, 7182818284 5904523536 0287471352
6
|
|
Voir Valeur des puissances de "e"
Voir Pi
/ Phi / Belle
formule
Relation avec les nombres premiers (p)
|
La fonction suivante tend vers e pour x tendant vers l'infini:
La convergence est très lente. |
Rang, premier, fonction
|
![]()
|
|
||
|
Maple – Direct
|
Le logiciel mathématique Maple dispose d'une instruction de calcul des
exponentielles. Et, exp(1
) = e. Évaluation (evalf) demandée avec
100 décimales et impression (lprint) |
|
|
Maple – Calcul avec factorielles
|
Utilisation de l'instruction d'addition (add)
de l'inverse des factorielles pour n de 0 à 100. |
|
|
Maple – Calcul optimisé avec
factorielles
|
Ce programme exploite la propriété de calcul
pratique qui évite de recalculer chaque factorielle complètement. En
effet:
|
|
Précision – Méfiance !
|
Maple
calcule avec la précision que vous voulez en:
Avec
Python, prenons des précautions. Ce logiciel ne calcule normalement qu'avec
16 chiffres significatifs. D'ailleurs, les calculs mathématiques ne font pas
partie du logiciel de base. Il faut faire appel au module mathématique (import math). Comment améliorer la précision des
calculs en Python ? Appel au module decimal.
Voir les programmes ci-dessous. |
PYTHON
|
Python – Direct
|
Avec Python, appel des logiciels de calcul mathématique (math). Demande d'impression de la constante e: résultat avec 16 chiffres
significatifs Demande de plus de chiffres ('.30g'):
les décimales proposées sont fausses (en jaune). |
|
Python – Calcul avec factorielles
|
Toujours avec le logiciel de mathématique (math),
on fait appel à l'instruction factorielle (factorial). La quantité d'itérations est précisée (quantité de termes) et la
valeur imprimée est arrondie avec cette quantité. Hélas, les derniers chiffres sont faux (en jaune). |
|
Python – Calcul optimisé avec
factorielles
|
Programme identique à celui écrit en Maple. Problème: ne fournit toujours que 16 décimales Même en demandant de lister 30 chiffres ('.30g),
les chiffres complémentaires sont faux (en jaune). |
|
Python – Calcul avec factorielles
et module decimal
2.7182818284 5904509079 5598298427
6488423347 47314453125 |
On appelle le module decimal
qui manipule de grands nombres en virgule
flottante. Un objet du type Decimal
est crée en utilisant la fonction decimal.Décimal. Notez les majuscules et minuscules. Alors, la valeur de e est connue avec autant de décimales
que l'on veut. Ici 40 décimales demandées. Elles sont toutes exactes. Voir Plus de décimales en Python |
Voir Programmation – Index
/ Python
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()