|
||||||||||||||||||||||||||||||||||||
Les quatre
opérations – Débutant
Voir / Évaluation de CM1
![]()
ESSENTIEL:
la soustraction vue autrement
selon les expert de l'enseignement

Humour
|
La
gamine dans la misère écrit: Papa Noël, je serais très contente si, cette
année, je pouvais obtenir 200 euros. Le
facteur compatissant décide d'organiser une collecte auprès de ses collègues
et récolte finalement 100 euros qu'il
dépose dans une belle enveloppe et l’envoie à la fillette. La
gamine remercie le Père Noël et ajoute: je voudrais tout de même te signaler
que ces voleurs de postiers en ont gardé la moitié.
|
|
Le
médecin à son patient: bonjour, j'ai deux
mauvaises nouvelles pour vous. D'abord, selon les analyses vous n'avez plus
que quarante-huit heures à vivre. Et
ensuite, ça fait deux jours que j'essayais
de vous joindre … Cette
annonce est sûrement négative (même fatale) pour le patient. Mais elle
témoigne surtout d'une soustraction : 2 – 2 = 0. |
|
Tout
le monde sait qu'en cas d'insomnie, il suffit d'additionner
mouton après mouton pour s'endormir. Mais combien de personnes savent que,
pour rester éveillé, il suffit de soustraire
les moutons. Everyone knows that if insomnia, simply add sheep
after sheep to fall asleep. But how many people know that to stay awake,
simply subtract the sheep? Les Marx Brothers |
|
Rien,
ce n’est pas rien ! La preuve, c’est que l’on peut le soustraire. Exemple : rien moins rien égal moins que rien ! - Raymond Devos, extrait du sketch
"Parler pour ne rien dire" |
|
-
Combien de fois peut-on soustraire 7 de 20 et quel est le reste ? -
Ben, je peux le soustraire
autant de fois que je veux et il restera toujours 13. |
Voir Pensées & humour
|
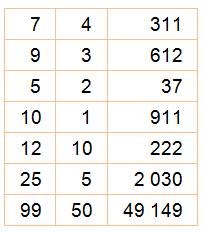
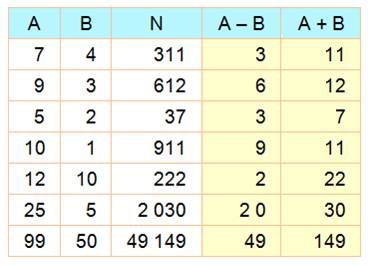
Quelle
est la logique de construction de ce tableau?
Avec
cette logique, si 7 + 4 donne 311 Trouvez
les valeurs de a et b telles que: a + b donne 123 |
|
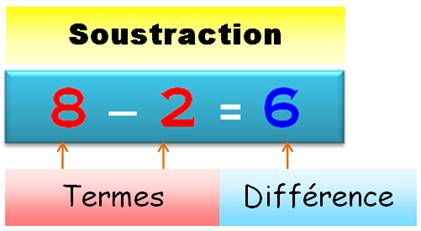
SOUSTRACTION – INITIATION
Principe de calcul
de la soustraction: Soustraction =
addition à trous ou addition à l'envers … Soustraction = addition de nombres
négatifs. Note: Une
fois la soustraction classique maitrisée par le débutant, ce qui lui paraît insurmontable
c'est l'étape suivante: la soustraction de nombres
négatifs.
|
Voir
Les quatre opérations – Junior
|
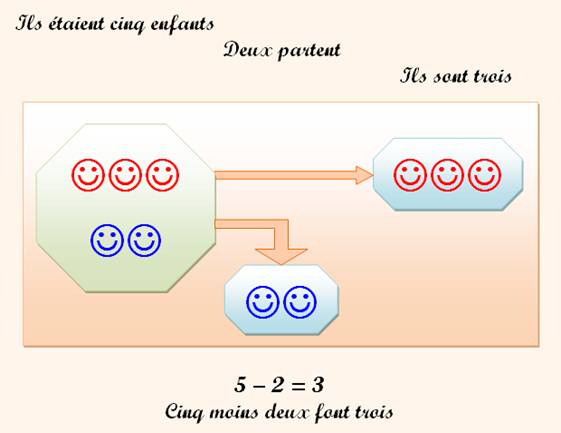
CINQ moins DEUX font TROIS |
|
|
On peut aussi dire que: entre maintenant et tout à
l'heure, il n'y a pas le même nombre d'enfants. La
différence est 2. |
|
Nombre moins la somme des chiffres = 9
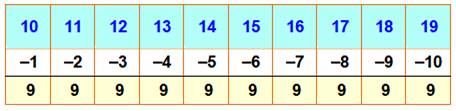
Voir Propriété générale /
Magie
du 9
Voir Cours de 5e / Puzzle arithmétique ou Cryptogramme
|
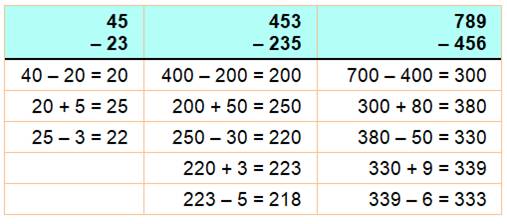
Le
but est d'obtenir les chiffres les plus "forts" (ceux à gauche) en
premier, contrairement au calcul classique de l'école. Alors je commence à
gauche et je récite mentalement les lignes indiquées ci-dessous dans le
tableau: 40 – 20 = 20 puis 20 + 5 = 25 et enfin 25 – 3 = 22. Etc.
Le
problème de la propagation de la retenue est simplifié. Autre
truc avec le complément à 10k >>> |
Voir Addition
/ Calcul mental
– Index
Problème qui trouble Internet et qui est à la portée d'un enfant
de 7 ans
|
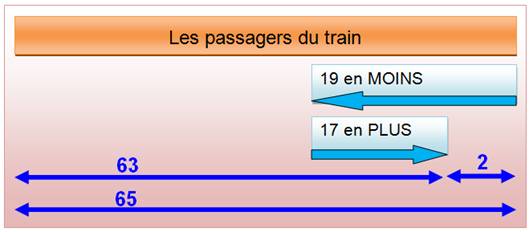
Problème À
cet arrêt, parmi les passagers du train, 19 en descendent et 17 montent. Ils
sont maintenant 63 à bord. Quel est le nombre de passager dans le train avant
l'arrêt. Solution Si
19 quittent et 17 arrivent c'est qu'il y a 2 passagers en moins dans le
train. On
avait P passagers avec 2 en moins, il y
en a 63; ils étaient donc 65. Illustration
|
Voir Autres problèmes troublant
Internet
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
EXEMPLE
TRÈS SIMPLE POUR COMMENCER
EXEMPLE
SIMPLE AVEC RETENUE
EXEMPLE
AVEC RETENUE
Maintenant traitons la colonne suivante, celle des dizaines.
On vérifie bien que 19 + 15 = 34. |
|||||||||||||||||||||||||||||||||||||||||||
|
RETENUES
EN CASCADE
Traitement de la colonne de droite, les unités.
Traitement de la colonne suivante, les dizaines.
Traitement de la colonne des centaines.
Traitement de la dernière colonne, celle des milliers.
On vérifie bien que 839 + 7 295 = 8 134 |
Les bonbons
|
Question: Clément et Alexis ont
chacun 10 bonbons. Clément
en a déjà mangé quelques uns et Alexis en a mangé autant que ceux qui restent
à Clément. Combien
ont-ils encore de bonbons à tous les deux ? Réponse:
la quantité de bonbons mangés est 10. En
effet: x + (10 – x) = x + 10 – x = 10 Il
en reste donc 10. |
|
|
||
|
Les
parenthèses sont parfois sans importance. C'est le cas avec les nombres
positifs et les additions. |
(1 + 2) – 3 = (3) – 3 = 3 – 3 = 0 |
|
|
Attention
on
ne peut pas interchanger (commuter) les termes de la soustraction. |
8 – 5 = 3 5 – 8 = – 3 |
|
|
Mais
souvent les parenthèses sont nécessaires et très importantes. Surtout
lorsqu'elles délimitent des paquets de nombres. Elles indiquent que ces
paquets forment un tout dont les opérations doivent être effectuées avant
toutes les autres. |
5 + (8 – 6) = 5 + (2) = 7 |
|
|
Retenir
qu'il faut traiter les opérations à l'intérieur des parenthèses en premier. |
(10–2) – (5–3) = (8) – (2) = 6 |
|
|
Dans
le cas de parenthèses encastrées, les plus profondes sont à traiter en
priorité. |
{(10 – 2 ) – (5 – 3)} – {(6 – 1)
– (9 – 7)} = {8 - 2} – {5 – 2} = 6 – 3 = 3 |
|
Suite Parenthèses
avec des nombres / avec des nombres
et des lettres
|
|
||
|
|
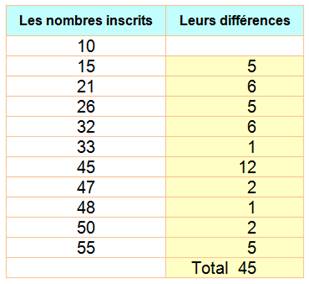
Avant que l'on me communique le résultat de la colonne de droite (45), je parie que je
peux le deviner. Je fais la soustraction 55 – 10 = 45 |
|
|
Ce tour de magie est bien simple (niveau primaire): La somme des écarts est égale à l'écart total. |
||
Tour mentionné dans Le
Magicien amateur – Magus – 1897 – Réédité en 2011
Faire tapisserie et oublier la soustraction
|
Luc
décide de retapisser son appartement comme d'ailleurs son voisin l'avait fait
avec le même appartement. À sa
demande, le voisin le renseigne: - Moi j'ai pris vingt-huit rouleaux. Luc
achète vingt-huit rouleaux de tapisserie et pose le papier. Constatant qu'il
a six rouleaux en trop, il retourne voir son voisin qui ne semble pas plus
étonné que cela. - Bizarre! Dit-il, moi aussi, c'est la même chose. |
Voir Pensées & humour
|
1)
Quelle est la logique de construction de ce tableau? Le
nombre N est formé par la concaténation de la différence et de la somme des
deux nombres des colonnes de gauche A et B.
2)
La logique étant celle-ci, alors a + b donne 123 veut dire que: (a
+ b) = 23 et (a – b) = 1 En
additionnant (a + b) + (a – b) = 2a = 24 a
= 12 et b = 11 |
Retour / Autres
énigmes de ce type / Les
folles énigmes du Net / Équations

Tu es sûr que je fais la
différence. Je suis positif.
![]()
|
|
||||||||||||
|
Des chercheurs de
l'Université de Genève (UNIGE) et de l'Université Bourgogne Franche-Comté
démontrent que notre capacité à résoudre des problèmes mathématiques est
influencée par nos connaissances. |
Ils ont montré que des mathématiciens de haut niveau peuvent se faire
piéger par certaines de leurs connaissances et échouent parfois à résoudre
des problèmes de simples soustractions. |
|||||||||||
|
Deux types de problèmes
selon la représentation faite des nombres: |
Nombres sur la droite des nombres (Classement
selon l'ordre: ordinal) ou Nombres représentés par des ensembles (Classement
selon la quantité: cardinal) |
|||||||||||
|
Exemples Réponse: 12 |
Droite des nombres Sarah a 14 animaux: des chats, et des chiens. Mehdi a 2 chats de moins
que Sarah, et autant de chiens qu'elle. Combien d'animaux Mehdi a-t-il ? Ensemble Lorsqu'il monte sur une table, le schtroumpf paresseux atteint 14
centimètres. Le schtroumpf grognon mesure 2 centimètres de moins que le
schtroumpf paresseux et il monte sur la même table. Quelle hauteur atteint le
schtroumpf paresseux ?". |
|||||||||||
|
Tests |
Les chercheurs ont proposé divers calculs basés sur des exemples
concrets pouvant être classés dans ces deux catégories et cela, à des
personnes non-mathématiciens et à des mathématiciens.
|
|||||||||||
|
Résultats |
On demandait si la solution proposée
était correcte ou s'il n'y avait pas de solution.
Toutes
les personnes mathématiciennes ou non ont plus de difficulté à résoudre les
problèmes avec représentations par des quantités (ensembles) que par des
nombres de type mesure. |
|||||||||||
|
Conclusion |
Ces résultats démontrent l'impact
crucial de nos connaissances du monde sur notre capacité à raisonner en
mathématique et la difficulté de changer de point de vue à la lecture d'un
énoncé. D'où l'importance de prendre en
compte ce biais dans l'enseignement. |
|||||||||||
Source: Une
simple soustraction piège des experts mathématiciens – Adrien – 11/07/2019
– Techno-Science.net
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |