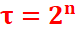NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 13/05/2018

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique     Brèves de Maths

     

DIVISION

 

Débutants

Division

DIVISEURS

 

Glossaire

Diviseur

 

 

INDEX

 

Décomposition

 

Généralités

Calculs

Facteurs  Premiers

Liste

2n Diviseurs

Communs

Records

Plus grand facteur

 

Sommaire de cette page

>>> Approche

>>> Généralisation 

>>> Valeurs 

>>> Récapitulatif 

>>> Avec les puissances

 

 

 

 

 

 QUANTITÉ DE DIVISEURS

Pricarielle

Cas où la quantité de diviseurs est: 

 et relation avec les nombres premiers !

 

La suite des nombres dont la quantité de diviseurs est une puissance de 2 est une pricarielle: produit des nombres premiers successifs ainsi que leur carré. Ex: 2 x 3 x 4 x 5 x 7 x 9 x 11…

Voir Primorielle

 

 

Rappel des notations

 

N

Nombre considéré.

 

F

Ses facteurs (N est le produit de ces nombres, cette décomposition est unique).

 

D

Diviseurs de N (N peut être divisé par un quelconque de ces nombres).

(tau)

Quantité de diviseurs y compris N.

(sigma)

Somme des diviseurs de N, y compris N lui-même.

Voir Diviseurs

  

Approche – Cas des diviseurs de 120

120

Facteurs

23 x 3 x 5

 

Diviseurs

1, 2, 3, 4, 5, 6, 8, 10,

12, 15, 20, 24, 30, 40, 60, 120

 

Quantité

16 = 24

 

120 est effectivement le plus petit nombre possédant 24 diviseurs. Quels sont les plus petits nombres possédant 2 n diviseurs ?

 

 

Somme

360

 

 

Plus petits nombres dont la quantité de diviseurs est 2n

= 2n

n

N

Facteurs

 

2

1

2

 

2

4

2

6

2 x

3

8

3

24

2 x 3 x

4

16

4

120

2 x 3 x 4 x

5

32

5

840

2 x 3 x 4 x 5 x

7

64

6

7 560

2 x 3 x 4 x 5 x 7 x

9

128

7

83 160

2 x 3 x 4 x 5 x 7 x 9 x

11

 

Les facteurs de N sont: les nombres premiers et leurs carrés.

 

2, 3, 4,  5, 7, 9, 11, 13, 17, 19, 23, 25, 29 …

 

 

 

 

 

Valeurs

F

2

6 =

 2 x 3

24 =

 2 x 3 x 4

120 =

 23 x 3 x 5

840 =

 23 x 3 x 5 x 7

D

1, 2

1, 2, 3, 6

1, 2, 3, 4, 6, 8, 12, 24

1, 2, 3, 4, 5, 6, 8, 10, 12,

15, 20, 24, 30, 40, 60, 120

1, 2, 3, 4, 5, 6, 7, 8, 10,

12, 14, 15, 20, 21, 24, 28, 30,

35, 40, 42, 56, 60, 70, 84, 105,

120, 140, 168, 210, 280, 840, 420

Q

2 = 2 1

4 = 2 2

8 = 2 3

16 = 2 4

32 = 2 5

S

3

12

60

360

2880

 

F

7 560 =

23 x 3 x 5 x 7 x 9

83 160 =

 23 x 33 x 5 x 7

 x 11

1 081 080 =

 23 x 33 x 5 x 7

 x 11 x 13

17 297 280 =

 23 x 33 x 5 x 7

 x 11 x 13 x16

D

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 21, 24, 27, 28, 30, 35, 36, 40, 42, 45, 54, 56, 60, 63, 70, 72, 84, 90, 105, 108, 120, 126, 135, 140, 168, 1512, 1080, 216, 360, 1260, 756, 210, 252, 3780, 280, 270, 630, 180, 189, 315, 1890, 840, 378, 420, 504, 540, 945, 7560, 2520

…

…

…

Q

64 = 2 6

128 = 2 7

256 = 2 8

512 = 2 9

S

28 800

345 600

4 838 400

82 252 800

 

 

 

 

 

 

 

 

 

Liste des valeurs pour N < 100

 

Chaque nombre N se déduit du précédent en le multipliant par le facteur indiqué.

Ainsi : 24 x 5 = 120.

 

= 2n

n

N

Facteur

2

1

2

2

4

2

6

3

8

3

24

4

16

4

120

5

32

5

840

7

64

6

7 560

9

128

7

83 160

11

256

8

1 081 080

13

512

9

18 378 360

17

1 024

10

349 188 840

19

2 048

11

8 031 343 320

23

4 096

12

200 783 583 000

25

8 192

13

5 822 723 907 000

29

16 384

14

180 504 441 117 000

31

32 768

15

6 678 664 321 329 000

37

65 536

16

273 825 237 174 489 000

41

131 072

17

11 774 485 198 503 027 000

43

262 144

18

553 400 804 329 642 269 000

47

524 288

19

27 116 639 412 152 471 181 000

49

1 048 576

20

1437 181 888 844 080 972 593 000

53

2 097 152

21

84793 731 441 800 777 382 987 000

59

4 194 304

22

517241 7617949847 420 362 207 000

61

8 388 608

23

346 551 980 402 639 777 164 267 869 000

67

16 777 216

24

24 605 190 608 587 424 178 663 018 699 000

71

33 554 432

25

1 796 178 914 426 881 965 042 400 365 027 000

73

67 108 864

26

141 898 134 239 723 675 238 349 628 837 133 000

79

134 217 728

27

11 777 545 141 897 065 044 783 019 193 482 039 000

83

268 435 456

28

1 048 201 517 628 838 788 985 688 708 219 901 471 000

89

536 870 912

29

101 675 547 209 997 362 531 611 804 697 330 442 687 000

97

 

 

Avec les puissances ? 

 

Liste des premiers et de leurs puissances jusqu'à 200

En rouge les puissances de nombres premiers

 

2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 23, 25, 27, 29, 31, 32, 37, 41, 43, 47, 49, 53, 59, 61, 64, 67, 71, 73, 79, 81, 83, 89, 97, 101, 103, 107, 109, 113, 121, 125, 127, 128, 131, 137, 139, 149, 151, 157, 163, 167, 169, 173, 179, 181, 191, 193, 197, 199.

 

 

Tentons le tableau en utilisant cette suite:

 

= 2n

n

N

Facteur

2

1

2

2

4

2

6

3

8

3

24

4

16

4

120

5

32

5

840

7

56

6

6 720

8 = 2 3

112

7

60 480

9

224

8

665 280

11

 

Avec 8, une puissance 3, ça ne marche pas ! Il faut dire que les facteurs sont la suite des nombres premiers et de leurs carrés. Et non pas, des nombres premiers et de leurs puissances, comme vu dans la littérature.

 

 

 

  

 

Suite

*   Facteurs  Premiers

*   Théorie des nombres – Diviseurs

*    Voir en haut de page

*    Liste des nombres et leurs facteurs et diviseurs

Voir

*    Calcul mental – Index

*    Diviseurs – Développements théoriques

*    Diviseurs – Somme en puissance

*    Divisibilité

*    Fonctions arithmétiques

*    Géométrie – Index

*    Machine des frères Carissan

*    Nombres composés

*    Nombres parfaits

*    PGCD

*    Premiers

*    Théorie des nombres – Index

*    Types de nombres selon leurs diviseurs

Cette page

*    http://villemin.gerard.free.fr/Wwwgvmm/Decompos/SigmaCal.htm