|
||||||||||||||||||||||||||||||||||||||||
![]()
|
|
|
||
|
Le produit de p nombres |
|
||
Rappel: la barre verticale se de lit: divise
Voir Application à la factorielle de la
somme
|
p = 2 |
2 | n (n + 1) |
|
C |
|
|
p = 3 |
6 | (n – 1) n (n + 1) = n3 – n |
|
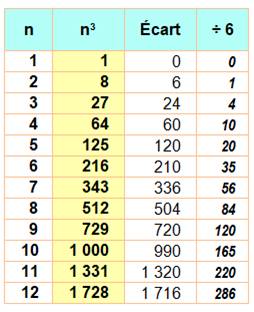
Propriété |
Un nombre
diffère de son cube par un multiple de 6.
Voir Nombre cube |
|
C
PAIR |
|
|
C
IMPAIR |
|
![]()
|
P = 4 |
24 | (n – 1) n (n + 1) (n + 2) |
|
C |
|
|
P = 5 |
120 | (n - 2)
(n - 1) n (n + 1) (n + 2) |
|
C
PAIRS |
|
|
C
IMPAIRS |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/CONSECUT/Recap.htm |
![]()