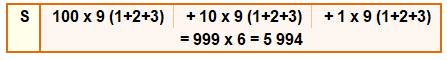Somme des nombres avec les chiffres 1, 2, 3 et 4

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/12/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	IDENTITÉS
Débutants Somme	SOMMES				Glossaire Addition
INDEX Narcissiques Somme-Produit Ch Formes et motifs Nombres en chiffres Chiffres Sommes de nombres Types de nombres Jeux et énigmes	S. de nombres	S. de chiffres	S. des entiers	S. des impairs
	S. de Nbs Démo.	S. de carrés	S. de cubes	S. de puissances
	Narcissiques	N + Somme Ch	S. des Ch de n^k	S. de factorielles
			S. des nombres en 1234
		Sommaire de cette page >>> Formulation et valeurs >>> Approche avec 12 et 123 >>> Sommes avec les chiffres de 1 à 9

SOMME des PERMUTATIONS

avec chiffres de 1 à q

Quelle est la somme de tous les nombres formés avec les chiffres 1, 2, 3 et 4 (par exemple); tous ou seulement les nombres à chiffres distincts ?

Il s'agit de la somme des nombres du type 1234 avec toutes ses permutations.

Le sujet général (avec chiffres répétés ou non) est traité à la page formes permutées.

Approche avec 12 et 123

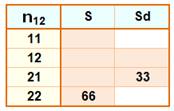
Chiffres 1 et 2

On peut former quatre nombres: 11, 12, 21, et 22.

Leur somme est 66, et celle des nombres à chiffres distincts est 33.

Chiffres 1, 2 et 3

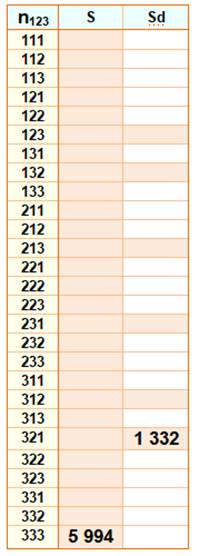
On peut former 27 nombres e 111 à 333, dont six seulement sont à chiffres distincts.

Dénombrements de la quantité de nombres

Dans le cas de tous les nombres, chaque chiffre peut prendre trois valeurs: Q = 3 x 3 x 3 = 3³ = 27.

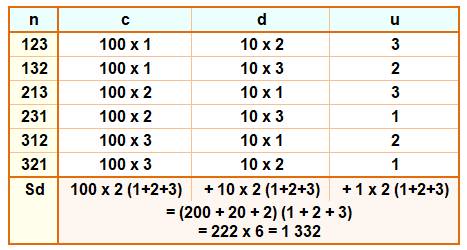
Dans le cas de chiffres distincts, le premier peut prendre trois valeurs, le deuxième deux valeurs et le troisième une seule: Qd = 3 x 2 x 1 = 3! = 6.

Calcul de la somme des nombres à chiffres distincts

Le tableau montre comment rapidement faire la somme de ces nombres; méthode pratique pour de plus grandes sommes.

Calcul de la somme de tous les nombres

Formulation et valeurs
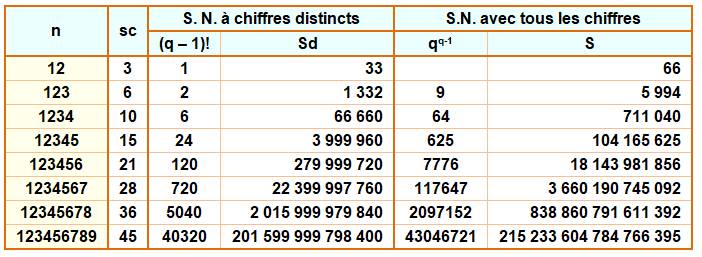
Somme des nombres à chiffres distincts Sd = (q – 1)! × 11…11_q × s Avec les chiffres de 1 à q La somme des chiffres est s. Le nombre en "1" contient q fois le "1" (à remplacer par (10^q – 1) / 9 pour une formule calculable directement).	Somme de tous les nombres S = q^{q – 1} × s Avec les chiffres de 1 à q La somme des chiffres est s.
Table de la somme des nombres permutés avec chiffres de 1 à q

Sommes avec les chiffres de 1 à 9
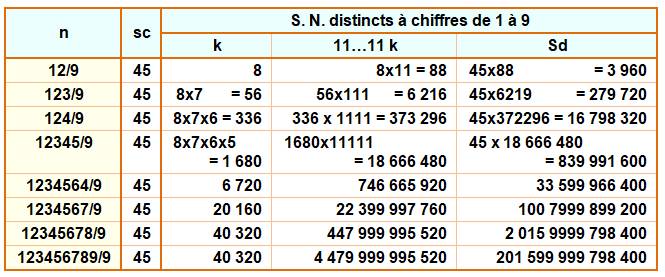
Tous les nombres à trois chiffres distincts parmi les chiffres de 1 à 9. 123, 124, 125, 126, 127, 128, 129, 132, …	Calcul du même type que précédemment impliquant la somme des chiffres 45. Avec trois chiffres le "1 " en première position apparait 8 x 7 fois (le "1" étant choisi, il a 8 possibilités pour le deuxième, puis 7 pour le troisième). Soit le calcul: (8 x 7) x 111 x 45 = 279 720.
Table pour les nombres de 2 à 9 chiffres Le dernier vaut: 45 x 8! x 111 111 111 = 201 599 999 798 400

Problème 126 de 536 Puzzles & Curious Problems de H.E: Dudeney

Ce problème traite de la somme des formes permutées distinctes à quatre chiffres: 1234 + 1243 + … = 66 660

La solution indique que pour les formes permutées distinctes des nombres à quatre chiffres en prenant tous les chiffres de 1 à 9 (et pas seulement de 1 à 4), la somme devient: 6 666 x 2 520 = 16 798 320, avec 2520 = 8 x 7 x 45.