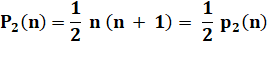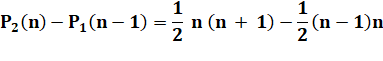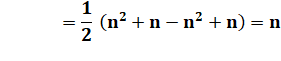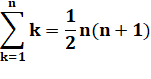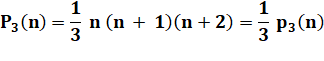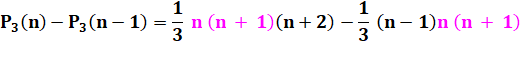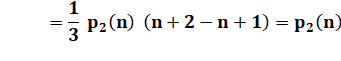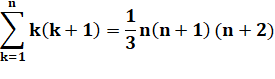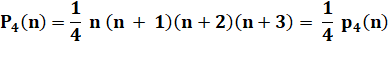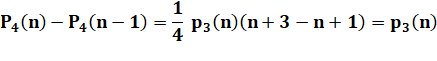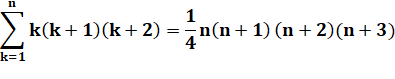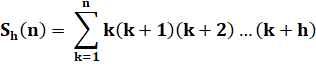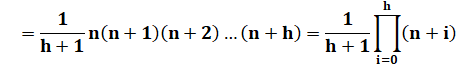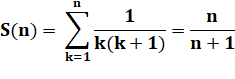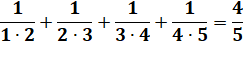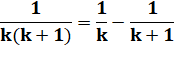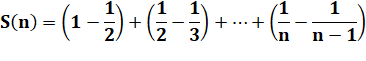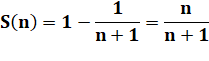|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMME de PRODUITS de nombres en progression arithmétique Cette page traite du calcul
de la somme de produits de nombres consécutifs à partir de 1, comme: 1 x 2 x
3 +
2 x 3 x 4 + … Exemple et règle pratique de calcul
Somme de n termes de h facteurs = fraction
1/(h+1) du produit commençant par n et comptant h+1 facteurs (c'est aussi le dernier terme avec
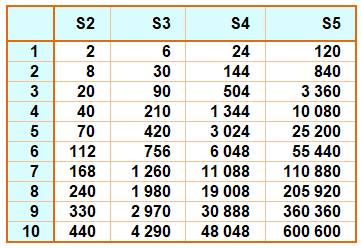
un facteur de plus) >>>. Table somme de 1 à 10 termes avec 2 à 5 facteurs. On
retrouve S2(4) = 40.
|
Voir Nombres
consécutifs / Somme
de nombres oblongs / Brève
556
|
|
||
|
Produit de deux nombres Somme des entiers |
|
|
|
La
différence |
|
|
|
Par
télescopage avec P2(0) = 0 (généralisation à tous les
n) |
|
|
|
Exemple
n = 5 |
1 + 2 + 3 + 4 + 5 = 1/2 (5 x 6) = 15 |
|
Voir Somme des nombres
entiers
Simplification par télescopage
|
Simplification d'une grande somme par annulation de termes deux à deux
ou alors de proche en proche.
Les P s'annulent deux à
deux. La somme des lignes est égale à
la somme des entiers. Elle vaut aussi P2 (n) = 1/2 n (n + 1). |
Voir Brève
590
|
Produit de trois nombres Somme des produits de deux nombres |
|
|
La
différence |
|
|
Par
télescopage avec P3(0) = 0 |
|
|
Exemple
n = 3 |
1x2 + 2x3 + 3x4 = 1/3 (3 x 4 x 5) = 20 |
|
Produit de quatre nombres Somme des produits de trois nombres |
|
|
La
différence |
|
|
Par
télescopage avec P4(0) = 0 |
|
|
Exemple
avec n = 3 |
1x2x3 + 2x3x4 + 3x4x5 = 1/4 (3 x 4 x 5 x 6) = 90 |
|
Produit de quatre nombres Somme des produits de trois nombres |
|
|
|
Exemple
avec h = 2 et n
= 4 |
1x2 + 2x3 + 3x4+ 4x5 = 1/3 (4x5x6) = 40 |
|
|
Exemple
avec h = 5 et n
= 5 |
1x2x3x4x5 + 2x3x4x5x6 + … + 5x6x7x8x9 = 1/6 (5x
6x7x8x9x10) = 25 200 |
|
|
Règle
pratique |
Le dénominateur de la
fraction est h + 1. Le produit commence
par n et compte h + 1 facteurs. Exemples S10 (6) =
1/11 (6.7.8.9.10.11.12.13.14.15.16) = 15 850 598 400 S10 (10) = 1/11 (10.11…
20) = 609 493
248 000 |
|
Voir Factorielle tronquée
|
|
||
|
Formule |
|
|
|
Exemple
n = 4 |
|
|
|
Démonstration par télescopage Avec cette identité: |
|
|
|
La somme devient: |
|
|
|
Les termes intermédiaires s'annulent deux à deux. |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/SPrPuiPA.htm |
![]()