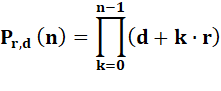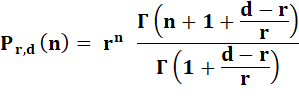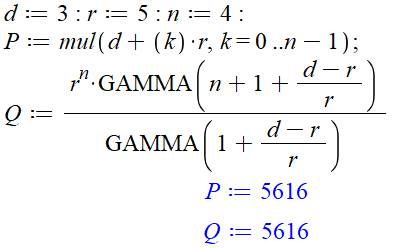NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/07/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	IDENTITÉS
Débutants Somme	SOMMES Nombres et puissances					Glossaire Addition
INDEX Sommes Calcul Identités	Index et Formules		Entiers	Carrés	Cubes
	Somme des puissances de nombres en progression arithmétique
	Produit de nombres en progression arithmétique
	Somme de produits de nombres en progression arithmétique
	Somme de produits – Méthode générale de calculs
		Sommaire de cette page >>> Produit de nombres en progression arithmétique >>> Exemples de calculs >>> Tables pour (r, d, n) de 1 à 10 >>> Bilan

PRODUIT des PUISSANCES

de nombres en progression arithmétique

(produit PNPA)

Nous connaissons les sommes de nombres en progression arithmétique.

Cette page traite du calcul du produit de nombres en progression arithmétique.

Exemple

Notation: P^p_{r, d} (n)

Produit de n termes en progression arithmétique de raison r, en commençant par le nombre de départ d.

La cas du produit porté à la puissance p est trivial: P^p_{r, d} = (P¹_{r, d})^p

Voir Nombres consécutifs

Produit de nombres en progression arithmétique
On cherche à calculer un produit tel que celui-ci: raison de la progression: r = 5 nombre de départ: d = 3 quantité de facteurs: n = 4	P5, 3 (4) = 3 x 8 x 13 x 18 = 5 616
Formule avec produit itératif On lit: produit des nombres (d + k.r) pour toutes les valeurs de k de 0 à n. Chaque facteur est la somme du nombre de départ (d) avec k fois la raison.
Formule de calcul direct Avec emploi de la fonction gamma (factorielles généralisées)
GAMMA (n) = (n – 1)! lorsque n est un nombre entier

Voir Lettres grecques

Exemples de calculs
Programme Avec implémentation des deux calculs
Autres exemples	P2, 2 (2) = 2 x 4 = 8 P2, 2 (10) = 2 x 4 x … x 20 = 3 715 891 200 P2, 10 (10) = 10 x 12 x … x 28 = 3 719 607 091 200 P3, 3 (3) = 3 x 6 x 9 = 162 P3, 10 (10) = 3 x 6 x … x 30 = 214 277 011 200

Bilan

Soit le produit compte un petit nombre de facteurs, alors le calcul à la main ou avec calculette est simple.

Soit la quantité de facteurs est importante, alors un logiciel s'impose, et le calcul peut être effectué classiquement avec la multiplication itérative ou avec la formule de calcul direct utilisant les factorielles (gamma).

Voir Table des produits pour {d, r, n} de 1 à 10 >>>

Retour	Somme des puissances de nombres en progression arithmétique
Suite	Somme de produits de nombres en progression arithmétique Somme des puissances des nombres successifs Somme des carrés des entiers successifs Somme des inverses Somme des puissances de 2 à 20 Somme des puissances successives Formules avec les puissances 4 Toutes les formules de somme Nombres de Bernoulli et sommes de puissances
Voir	Identités remarquables – Formulaire Nombres consécutifs Index Nombres de Bernoulli Nombres géométriques Pairs et impairs Somme des puissances des nombres successifs - Holopotentiel Tautochronie
Sites	How to find the product of n terms of an arithmetic progression – Mathematics
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/MulPuiPA.htm