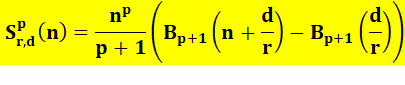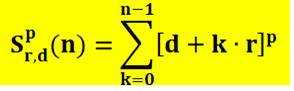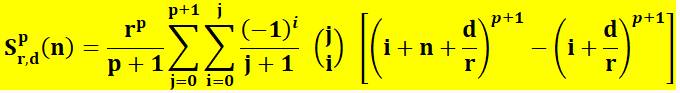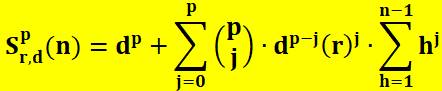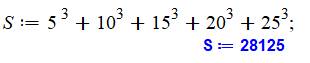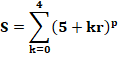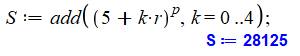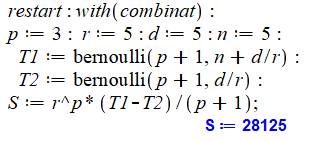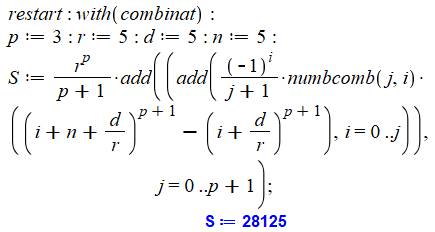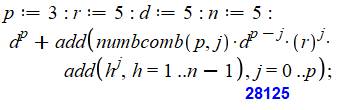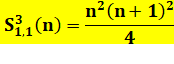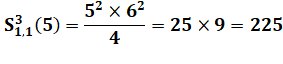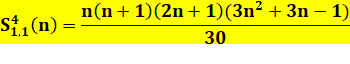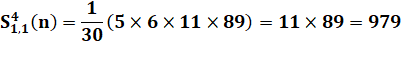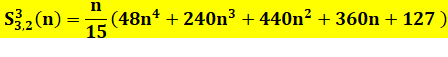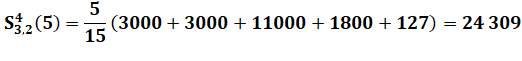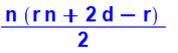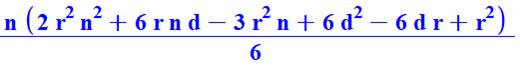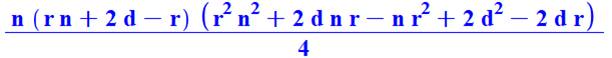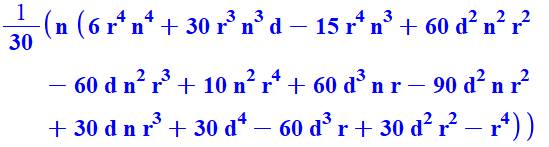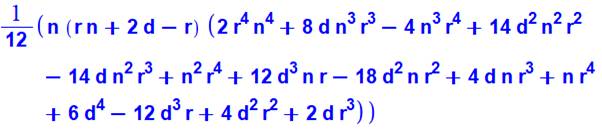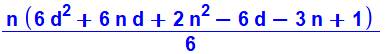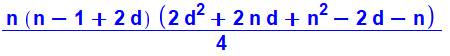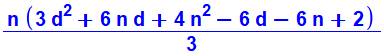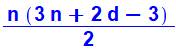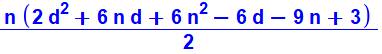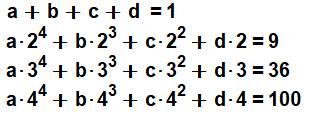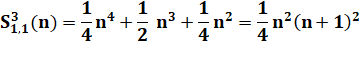|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES des PUISSANCES de nombres en progression arithmétique (somme PNPA) Les
sommes classiques des nombres successifs ont
déjà été vues. On connait les formules de calcul
de la somme des nombres successifs à une certaine puissance. Cette
page traite du calcul de la somme de nombres en progression
arithmétique, chacun porté à la même puissance. Exemple
Notation: Spr,
d (n) Somme de n
termes à la puissance p en partant de d et avec une progression arithmétique
de raison r. |
Voir Nombres
consécutifs
|
Deux types de questions:
Après énoncé des formules, analyse progressive de cas courants. |
|
|
||
|
Formule générale produisant la somme
directement. Elle utilise les polynômes
de Bernoulli. |
|
|
Exemples de calcul avec ces formules
|
1) Calcul
explicite de S35, 5 (5) |
|
|
|
2) Calcul
avec sommation itérative Rappel: la somme
itérative se
note:
|
|
|
|
3) Calcul
avec la formule "Bernoulli" |
|
|
|
4) Calcul
avec la formule en double sommation de Cereceda |
|
|
|
5) Calcul
avec la seconde formule de Dekpe |
|
|
|
Conclusion |
Quitte à utiliser un logiciel, la formule itérative
classique est encore la plus simple ! |
|
Voir Programmation – Index
![]()
Formulation polynômiales
dans les cas simples
|
|
|||
|
Nombres successifs à partir de 1. |
|||
|
On
connait la somme des cubes (ou autres puissances) des
nombres successifs. |
|
||
|
Autre
exemple avec les bicarrés |
|
||
|
Nombres en progression arithmétique
à partir de d |
|||
|
Le calcul
explicite: Et, si on
voulait une formule pour le cube, la
voici: |
|
||
|
Formule
pour les bicarrés en partant de 3 et en progressant de 2 ? Ça se complique ! |
|
||
Formules générales pour
les puissances de 1 à 5
![]() n est bien la quantité
de termes dans la somme (et non le terme final)
n est bien la quantité
de termes dans la somme (et non le terme final)
|
p |
Formules Exemples avec n = 5,
d = 10 et r = 5 |
|
1 |
10 + 15 + 20 + 25 + 30 = 1/2 (5 x (25 + 20 – 5) )
= 1/2 (200) = 100 |
|
2 |
102 + 152 + 202
+ 252 + 302 = 2 250 |
|
3 |
103 + 153 + 203
+ 253 + 303 = 55 000 |
|
4 |
104 + 154 + 204
+ 254 + 304 = 1 421 250 |
|
5 |
105 + 155 + 205
+ 255 + 305 = 38 150 000 |
|
Type |
Nom |
Formules Exemples avec n =
5, d = 10 |
|
Somme des
entiers, pairs et impairs |
|
10 +
11 + 12 + 13 + 14 = (5 x 24) / 2 = 60 |
|
Somme des
carrés |
|
102
+ 112 + 122 + 132 + 142 = 5 (876)
/ 6 = 730 |
|
Somme des
cubes |
|
103
+ 113 + 123 + 133 + 143 = 5 (24)
(300) / 4 = 900 |
|
Somme r = 2 pairs et
impairs |
|
|
|
– au carré |
|
102
+ 122 + 142 + 162 + 182 = 5 (612)
/ 3 = 1 020
22
+ 42 + 62 + 82 + 102 = 10 (6 x
11) / 3 = 220
12
+ 32 + 52 + 72 + 92 = 5 (9 x 11)
/3 = 165 |
|
– au cube |
|
103
+ 123 + 143 + 163 + 183 = 5 (14)
(220) = 15 400
23
+ 43 + 63 + 83 + 103 = 50 x 36 =
1 800
13
+ 33 + 53 + 73 + 93 = 25 x 49 = 1
225 |
|
Somme des
multiples de 3 |
|
10 + 13 + 16 + 19 + 22 = 5 (32) / 2 = 80 |
|
– au carré |
|
102 + 132 + 162 + 192
+ 222 = 5 (548) / 2 = 1 370 |
|
– au cube |
|
103 + 133 + 163 + 193
+ 223 = 5 (32) (620) / 4 = 24 800 |
![]()
Voir
Table des
sommes pour {p, d, r} de 1 à 5 et n de 1 à 10 >>>
|
|
||
|
Calcul de S31, 1 (n), par exemple Le polynôme sera de degré p + 1 = 4 Pas de terme constant (S(0) = 0) Forme générale Résolution avec connaissance de quatre points:
(1, 9, 36, 100). |
Équations
Solution
|
|
![]()
|
Retour |
|
|
|
|
|
Table |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomPuiPA.htm
|
![]()