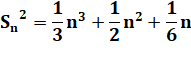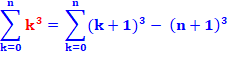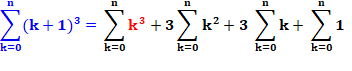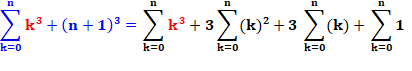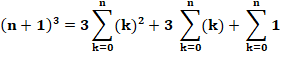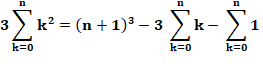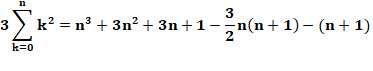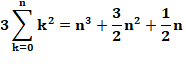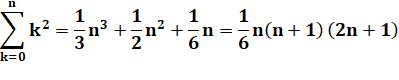NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/07/2022 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	IDENTITÉS
Débutants Somme	SOMMES des entiers, carrés … DÉMONSTRATIONS			Glossaire Addition
INDEX Sommes de 1 à n Addition Identités	Démonstrations directes		Démonstrations par induction
	Démonstrations avec équations		Démonstration par sommation
		Sommaire de cette page >>> Somme des entiers – Méthode des différences >>> Somme des carrés – Méthode des différences >>> Somme des carrés – Méthode de la sommation

Somme des entiers à une puissance

DÉMONSTRATION avec ÉQUATIONS

Méthode des différences

Nous abordons le troisième type de démonstration des formules donnant la somme des entiers, des carrés, des cubes, etc.

Variante de la démonstration directe consistant à:

observer les valeurs de départ pour n = 1, 2, 3 …

noter leurs différences successives;

déterminer la forme de l'équation correspondante; et

calculer les coefficients de l'équation.

Somme des entiers – Méthode des différences
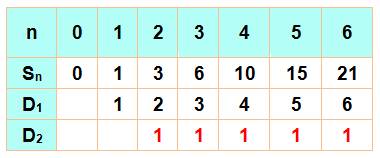
Table des différences Sn est la somme (le cumul) des nombres de 1 à n. D1 est la différence entre le nombre au-dessus et le précédent. D2 est la seconde différence. Elle est constante et égale à 1.
La somme des entiers est quadratique (du deuxième degré) car D2 = constante.	Sn = ax² + bx + c
Valeurs prises par Sn pour n= 1, 2 et 3	S0 = 0 = a(0)² + b(0) + c = c S1 = 1 = a(1)² + b(1) + 0 = a + b S2 = 3 = a(2)² + b(2) + 0 = 4a + 2b
Résolution	S2 = 3 = 4a + 2b –2 S1 = –2 = – 2a – 2b 1 = 2a
Équation	c = 0 a = 1/2 b = 1/2 Sn = 1/2x² + 1/2x = ½ x ( x + 1)

Voir Machines de Babbage / Différences secondes constantes

Somme des carrés – Méthode des différences
Table des différences Sn^2 est la somme (le cumul) des carrés des nombres de 1 à n. Disont les différences successives. D2 est constante
La somme des carrés des entiers est du troisième degré car D3 = constante.	Sn^2 = ax^3 + bx^2 + cx + d
Valeurs prises par Sn^2 pour n= 1, 2, 3 et 4	S0^2 = 0 = d S1^2 = 1 = a + b + c S2^2 = 5 = 8a + 4b + 2c S3^2 = 14 = 27a + 9b + 3c
Résolution du système d'équations
Équation

Voir Même chose avec différences finies et coefficients binomiaux /
Somme de produits – Méthode des différences

Bilan

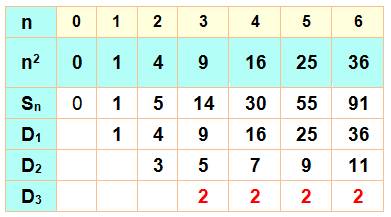
La même méthode s'applique au calcul des puissances d'ordre supérieur.

Somme des carrés – Méthode de la sommation
Méthode originale qui passe d'abord par la somme des cubes pour en déduire la somme des carrés.
Somme des cubes de rang n comme somme de ceux de rang n + 1 moins le cube du dernier.
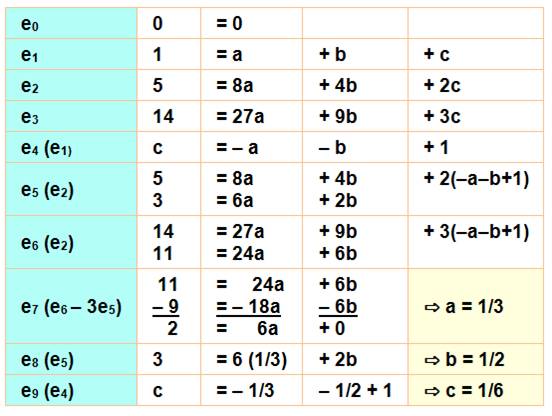
Justification de cette formule avec un exemple: n = 3. Notez que 0^k = 0; ne pas confondre avec 0! = 1		0^3 + 1^3 + 2^3 + 3^3 = 1^3 + 2^3 + 3^3 = (0+1)^3 + (1+1)^3 + (2+1)^3 + (3+1)^3 – 4^3 = 1^3 + 2^3 + 3^3 + 4^3 – 4^3 = 1^3 + 2^3 + 3^3
Développement de (k + 1) au cube (identité remarquable du cube).	(x + 1)^3 = x^3 + 3x^2 + 3x + 1
Remplaçons la somme en k+1 par celle en k (égalité vue ci-dessus en bleu).
Les termes en k au cube s'éliminent. Et, en évaluant le terme en carré:
En développant: Notez que somme de 0 à n des "1" vaut bien n+1 et non n (le 1 en position 0 compte).
Collecte des termes semblables:
En divisant par 3:

Merci à G.S. pour sa lecture attentive

Bilan

Il se trouve que cette méthode marche pour toutes les puissances supérieures et y compris pour la somme des entiers.

Retour	Démonstrations directes Somme des nombres de 1 à n – Index
Suite	Somme des entiers Somme de cube – Général Somme de cubes – Table Somme des impairs, carré et cubes Somme de produits – Méthode des différences
Aussi	Somme des nombres – Récapitulatif Somme des chiffres Démonstration par récurrence - Principe
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomDemo2.htm