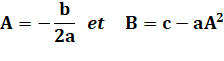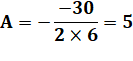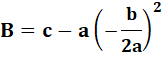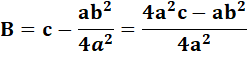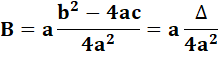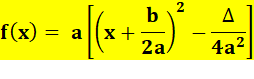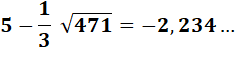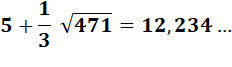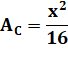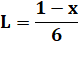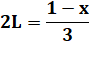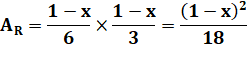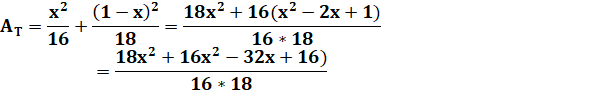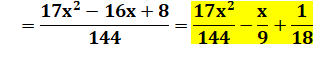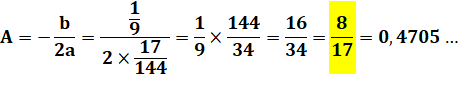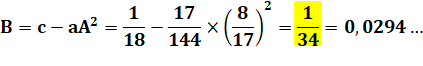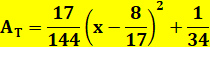|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
ÉQUATIONS du 2e degré ou Équation du second degré ou Équation quadratique ax² + bx + c = 0 L'équation
du deuxième degré possède deux racines, mais pas toujours des racines en
nombres réels. Elles peuvent complexes. S'il vous plait, la solution, tout de
suite! >>>
Si
elle est bien comprise l'équation du deuxième degré n'a plus aucun secret. |
Anglais:
Quadratic
equation
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Problème
Quelle est la taille du terrain ? Paramétrage
Solution
Réponse: le fermier possède un terrain
carré de 10 m de côté Remarque L'astuce a consisté à remarquer que x² + 4x est le début du développement d'un carré remarquable:
(x + 2)² = x² + 4x
+ 4. Dans ce cas, il y a
une solution évidente: x²
+ 4x = x (x + 4) = 140 Il
faut trouver deux diviseurs
de 140 séparés de 4 unités. On
trouve facilement: x = 10 et x + 4 = 14. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Exercices
d'initiation (classe de seconde)
|
|
|
|
|
|
|
|
||||
|
Le trinôme ou forme
polynomiale du second degré peut s'écrire de trois façons. |
||||
|
Forme développée |
|
Usage: calcul de limite, de dérivée, d'intégrale. |
||
|
Forme factorisée |
|
Avec les deux racines réelles lorsqu'elles existent. Usage: étude de signe |
||
|
Forme canonique |
|
Usage: introduction du discriminant: b² - 4ac |
||
|
Exemple de mise sous forme canonique |
||||
|
Fonction |
|
|||
|
Mise en facteur de a |
|
|||
|
Recherche du début d'un carré |
|
|||
|
On recolle avec notre trinôme, puis calculs |
|
|||
|
Alternative de calcul |
|
|||
|
En rapprochant la forme développée de la forme canonique |
|
|||
|
En égalant les termes semblables |
|
|||
|
Soit les valeurs de A et B |
|
|||
|
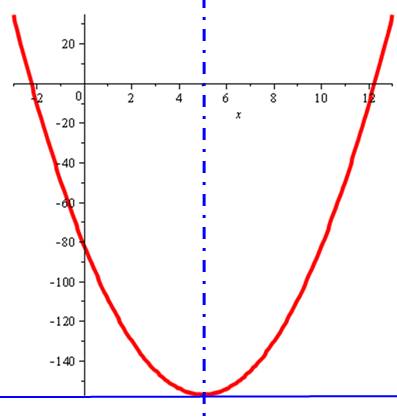
Application numérique Le point de coordonnées (A, B) est le point d'extremum de la parabole.
Celle-ci est symétrique par rapport à la verticale d'abscisse x = 5 |
|
|||
|
Forme canonique explicitée |
||||
|
Poursuivons nos calculs en remplaçant A dans l'expression en B |
|
|||
|
En remplaçant A et B par leurs valeurs |
|
|||
|
Pour information: La parabole Sommet (5, -157)
|
|
|
|
||||||
|
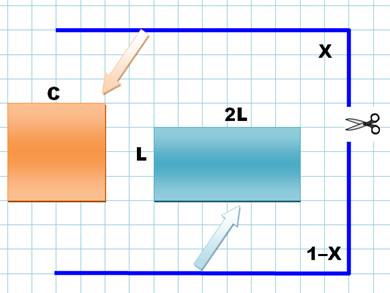
Une ficelle de 1 mètre de
long. On en coupe un morceau de
longueur x. Avec ce morceau on forme un
carré; avec l'autre, un rectangle deux fois plus long que large. On cherche la valeur de x telles
que les deux figures présentent une aire totale minimale. |
|
|||||
|
Carré |
P = 4c = x |
|
|
|||
|
Rectangle |
P = 6L = 1 – x |
|
|
|||
|
Aire totale |
|
|||||
|
Forme canonique |
|
|||||
|
|
||||||
|
|
|
|||||
|
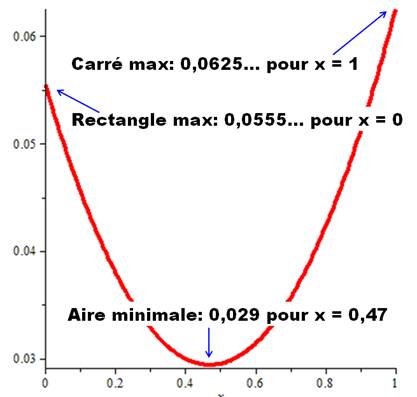
Bilan L'aire est minimale pour x = 8/17 = 0,47 … C'est là qu'il faut donner le coup de ciseau. L'aire totale vaut: 1/34 = 0,029 m². Côté du carré: 2/17 = 0,117… m Largeur du rectangle: 3/34 = 0,088… m C'est avec le carré seul (x = 1) que l'aire est maximale (A = 1/16 =
0,0625) |
||||||
![]()
|
Suite |
|
|
Différences
secondes constantes ax² + bx + c |
|
|
Voir |
|
|
Cette page |
![]()