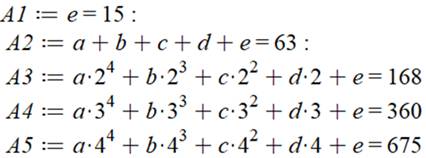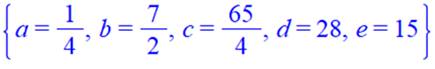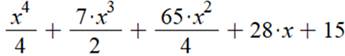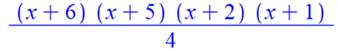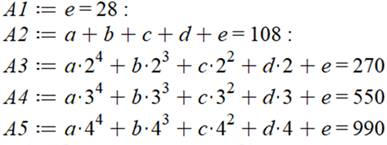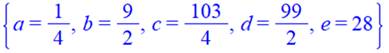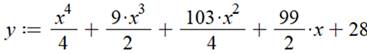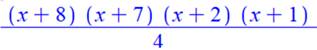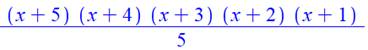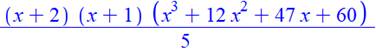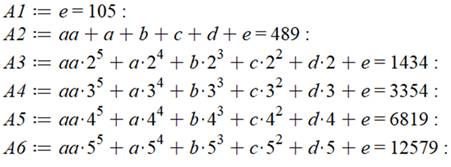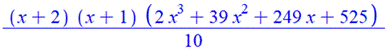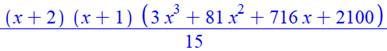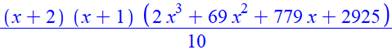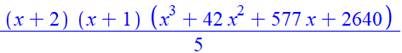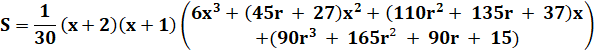Somme de produits, Méthode générale de calculs

Édition du: 11/08/2022

INDEX Sommes Calcul Identités	Somme de produits
	Index et Formules	Entiers	Carrés	Cubes
	Somme des puissances de nombres en progression arithmétique
	Produit de nombres en progression arithmétique
	Somme de produits de nombres en progression arithmétique
	Somme de produits – Méthode générale de calculs

Faites un double-clic pour un retour en haut de page

SOMME de PRODUITS

Méthode générale de calculs

SOMME de n termes, chacun produit de k nombres en progression arithmétique de raison r.

Pour les cas les plus simples, il existe des formules. Pour les cas spécifiques très nombreux, la formule n'existe pas dans les livres. Il faut la calculer. Comment ?

Par la méthode des différences finies et une mise en équation.

Sommaire de cette page

>>> Somme 1×3×5 + …

>>> Somme en (n)(n+r)(n+2r)

>>> Somme en (n)(n+r)(n+2r)(n + 3r)

Débutants

Somme

Glossaire

Addition

Voir Somme des entiers et somme des carrés avec la méthode des différences

Somme 1×3×5 + 2×4×6 + 3×5x7 … (n)(n+r)(n+2r)

haut

Calcul des premiers cas

Somme de n produits de trois nombres en progression arithmétique de raison r = 2.

1x3x5 = 15

1x3x5 + 2x4x6 = 15 + 48 = 63

1x3x5 + 2x4x6 + 3x5x7 = 63 + 105 = 168

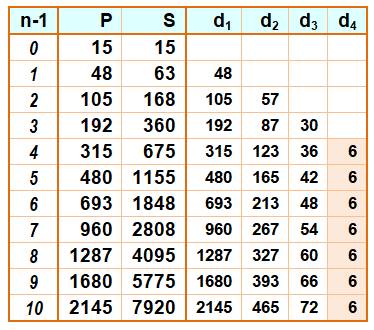
Tabulation et calcul des différences

Le premier terme (1x3x5) est noté avec l'indice 0 soit n – 1.

La colonne 2 donne le produit n(n+2)(n+4). Pour n = 3 soit: 3x5x7 = 105.

La colonne 3 indique la somme cumulée.

Viennent ensuite quatre colonnes de différences entre les valeurs successives. Ainsi: 48 = 63 – 15 ou encore 30 = 87 – 57.

Propriété

La différence d'ordre 4 est constante (égale à 6), S est une fonction du quatrième degré.

Pour connaitre la valeur de chacune des constantes, il faut cinq exemples d'équations.

Choisissons les cinq premières lignes du tableau

S = an⁴ + bn³ + cn² + dn + e

Résolution

La résolution d'un système de cinq équations est un peu laborieuse.

Faisons appel à un logiciel de calcul.

Et avec ces coefficients dans l'équation générique:

Factorisation

Exemple x = 10

S = 16 x 15 x 12 x 11 / 4 = 7 920

S =

Somme en (n)(n+r)(n+2r)		haut
Cas de r = 3 Premier terme: 1x4x7 = 28 Deuxième: 28 + 2x5x8 = 108 … Ci-contre, les mêmes étapes que précédemment pour aboutir à une factorisation qui ressemble à celle obtenue pour r = 2.
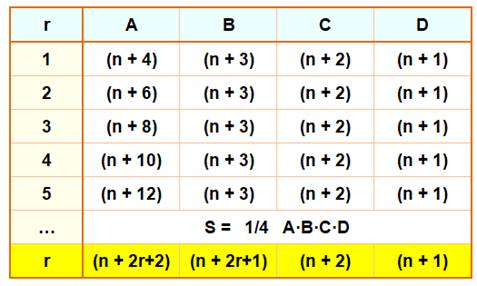
Formule générale pour r quelconque Somme de n produits de trois nombres en progression arithmétique de raison r. Le formule générale est de la forme: S = (n + 2 r + 2) (n + 2r + 1) (n + 2) (n + 1)

Somme en (n)(n+r)(n+2r)(n + 3r)

haut

Cas de r = 1

Premier terme: 1x2x3x4 = 24

Deuxième: 24 + 2x3x4x5 = 144

Formule, tous calculs faits, voir la suite pour explications

S₁ =
S₁ =

Cas de r = 2

Premier terme: 1x3x5x7 = 105

Deuxième: 105 + 2x4x6x8 = 489

…

Le calcul des différences montre que, cette fois, la différence cinquième est constante. La formule pour S sera de degré 5.

Ci-contre, les mêmes étapes que précédemment pour aboutir à une factorisation comportant un facteur du troisième degré.

S₂ =

Cas de r de 3 à 6

Formules calculées et factorisées ci-contre.

On a deux facteurs communs (x + 2) (x + 1) et un facteur du troisième degré.

S₃ =
S₄ =
S₅ =
S₆ =

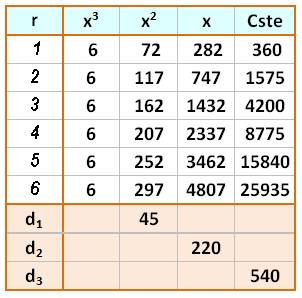
Pour calculer la formule générale

Il faut traiter le polynôme du troisième degré en procédant comme suit:

Normaliser ses coefficients en mettant toutes les fractions au dénominateur 30. Ce qui donne ce tableau.

Calculer les différences successives.

Écrire et résoudre les équations qui donnent la formule pour chacun des coefficients.

Terme en x³ : 6

Terme en x² : 45r + 27

Terme en x : 110r² + 135r + 37

Terme constant: 90r³ + 165r² + 90r + 15

Formule générale

S est la somme de x+1 termes, chacun produit de quatre facteurs en progression arithmétique de raison r, commençant par 1.

Quelques valeurs

x= 0 veut dire qu'il y a un terme comme avec r = 1: 1x2x3x4 = 24

x= 0 veut dire qu'il y a deux termes comme avec r = 3: 1x4x7x10 + 2x5x8x11 = 1160

Haut de page

Retour	Somme de produits de nombres en progression arithmétique Somme des puissances de nombres en progression arithmétique
Suite	Somme des puissances des nombres successifs Somme des carrés des entiers successifs Somme des inverses Somme des puissances de 2 à 20 Somme des puissances successives Formules avec les puissances 4 Toutes les formules de somme Nombres de Bernoulli et sommes de puissances
Voir	Identités remarquables – Formulaire Nombres consécutifs – Index Nombres de Bernoulli Nombres géométriques Pairs et impairs Somme des puissances des nombres successifs - Holopotentiel Tautochronie
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomProGe.htm