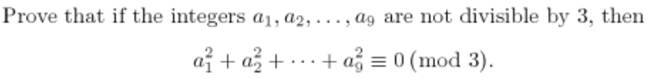NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/12/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	PUISSANCES
Débutants Nombres géométriques	CARRÉS				Glossaire Nombres carrés
INDEX Nombres carrés, cubes … Puissances	Index	Introduction	Formes	Écarts
		Caractérisation	Carré mod 3	Unités
		Sommaire de cette page >>> Approche et rappels >>> Somme de deux carrés en mod 3 >>> Somme de trois carrés en mod 3 >>> Somme de quatre carrés en mod 3

Sommes de CARRÉS mod 3

Divisibilité des carrés et de leurs sommes par 3.

Une somme de deux carrés est divisible par 3,

si chacun des deux nombres est divisible par 3.

Approche et rappels sur les carrés
Mod 2	Le carré conserve sa parité.	2² = 4 pair 3² = 9 impair
Mod 3	Le carré d'un multiple de 3 est divisible par 3; pout tous les autres le reste est égal à 1.	2² = 1 x 3 + 1 3² = 3 x 3 + 0 4² = 5 x 3 + 1 5² = 8 x 3 + 1 6² = 13 x 3 + 0

Voir Carrés modulo de 2 à 12

Somme de deux carrés en mod 3
Deux carrés	La somme de deux carrés est divisible par 3 si chacun des deux nombres est divisible par trois.
Démonstration	Pour A Pour B Alors pour A + B Seul cas pour un résultat nul	A mod 3 = {0, 1} B mod 3 = {0, 1} (A + B) mod 3 = {0, 1, 2}
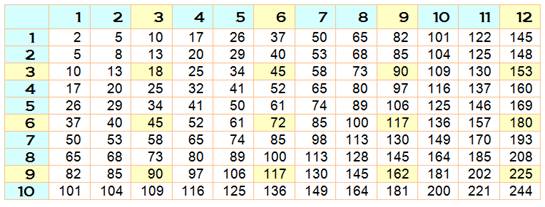
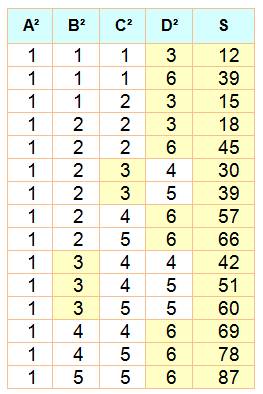
Exemples	Les seuls cas où la somme des deux carrés est divisible par 3 se trouvent aux croisement des lignes et colonnes de nombres divisibles par 3.

Somme de trois carrés en mod 3
Deux carrés	La somme de trois carrés est divisible par 3 si chacun des deux nombres est divisible par trois ou si aucun ne l'est.
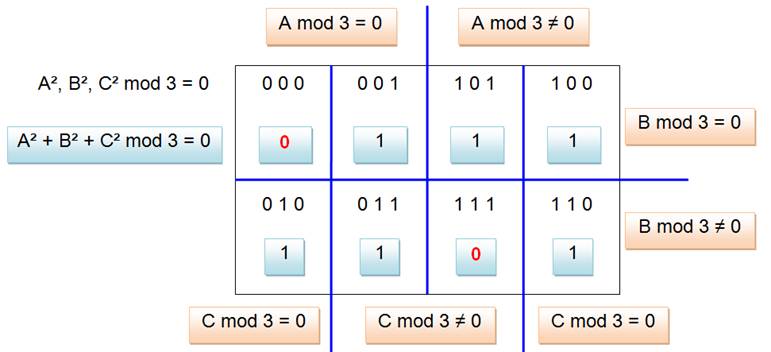
Démonstration	Un bon moyen de visualiser tous les cas et ne rien oublier consiste à faire un diagramme: un rectangle est partagé en deux parties: à gauche le cas où A est divisible par 3 (A mod 3 = 0); et à droite le cas où il n'est pas divisible (A mod 3 = 1 ou 2); l'ensemble est partagé horizontalement en deux avec la même logique pour la divisibilité de B; et encore un partage vertical pour la divisibilité de C. Dans chacune des huit cases créées: en haut, les trois chiffres indique la valeur de A², B² et C² modulo 3, sachant qu'un carré modulo 3 vaut seulement 0 ou 1: et en bas, la valeur de la somme de ces modulos. On se souvient que 3 mod 3 = 0.
Exemple de lecture:	Dans la case en haut à gauche pour A = B = C = 0 mod 3 en haut: A² mod 3 vaut 0. c'est le cas aussi pour B² et c², soit 0 0 0 en bas, la somme 0 + 0 + 0 = 0
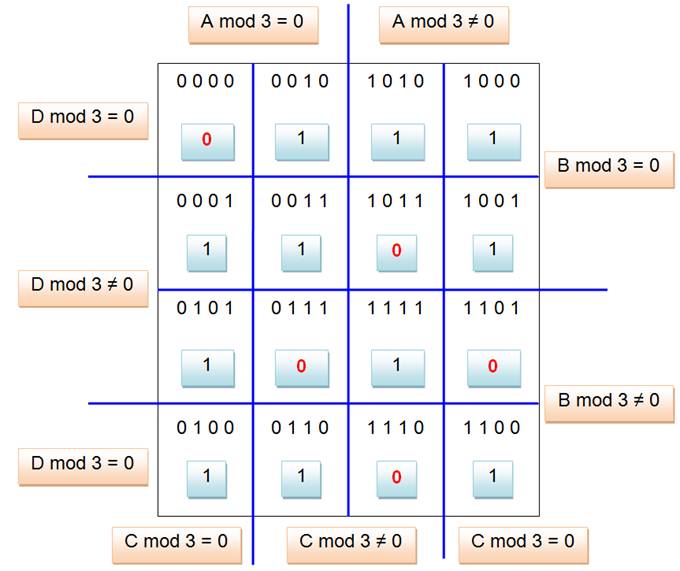
Conclusions	Cette case du haut à gauche, avec 0, témoigne du fait que, si les trois nombres sont divisibles par trois, la somme des carrés l'est aussi. La deuxième case marquée 0 témoigne, elle, du fait que, si les trois nombres ne sont pas divisibles par 3, alors la somme de carrés est tout de même divisible par 3. Les autres cases indiquent que dès qu'un nombre n'est pas divisible par 3, à l'exception des trois à la fois, alors la somme des carrés n'est pas divisible par 3.
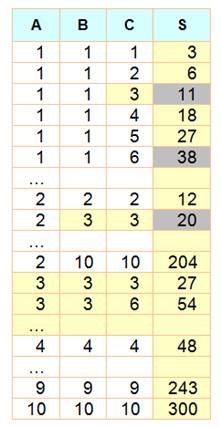
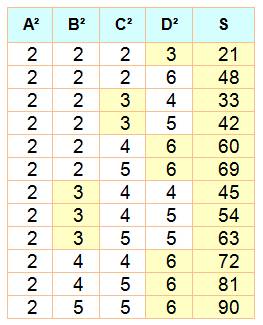
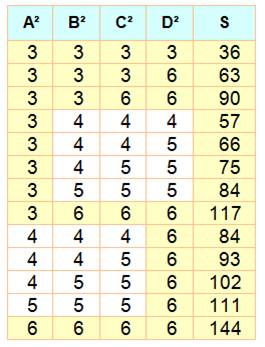
Exemples	En jaune les nombres divisibles par 3 et en gris les non-divisibles pour S = A² + B² + C². Dés qu'un ou deux nombres parmi A, B ou C est (sont) divisible(s) par 3, la somme des carrés ne l'est pas. Par contre si les trois le sont, la somme l'est.

Somme de quatre carrés en mod 3
Voici le diagramme de Karnaugh pour la somme de quatre carrés. Une somme de quatre carrés est divisible par 3, si tous les nombres sont divisibles par 3 ou si un seul est divisible et les trois autres non. Exemples

Propriété

Les sommes de la forme (a² + b² + …) comportant une quantité de termes multiple de 3 et dont chaque nombre n'est pas divisible par 3, sont divisibles par 3.

Exemple: 1² + 2² + 4²+ 5² + 7² + 8²+ 10² + 11² + 13² = 549

Exemple de problème posé

Suite	Carrés mod 4 et 8
Nombres géométriques	Allumettes et nombres carrés Introduction Théorie Valeurs
Voir	Calcul des carrés Calcul du carré des impairs Carré en géométrie Carrés – Calcul mental Carrés – Somme de carrés Carrés – Somme des carrés des consécutifs Carrés – Variations sur - Carrés magiques Identité de Brahmagupta Nombres à motifs Nombres carrés – Glossaire Nombres carrés – Nomenclature
Cette page	http://villemin.gerard.free.fr/aNombre/FIGURE/CarreMo3.htm