loi de la logique, fonction addition

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/12/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Rubrique LOGIQUE
Débutants Logique	Lois de la LOGIQUE				Glossaire Logique
Inversion		ET	OU	Implication
Phrases			OU Exclusif	Équivalence
		Multi-variable	Addition
Sommaire de cette page >>> Addition en binaire >>> Additionneur 1 bit >>> Retenue >>> Observations >>> Circuit logique de l'additionneur >>> Addition n bits >>> Anglais

Logique et addition

Comment réaliser un additionneur

Explications pas à pas

Addition en binaire

On se souvient de comment réaliser une addition en numération binaire.

on donne l'exemple pour un seul chiffre (un bit).

puis, pour l'opération 5 + 6.

on recommence avec 5 + 7.

On remarque qu'il faut savoir:

faire l'addition sur un bit comme indiquée en haut à droite;

donner la place à un nouveau chiffre en fin de calcul (addition 5 + 6); et

d'une manière générale, tenir compte de la retenue tout au long du calcul (addition 5 + 7).

Addition en binaire de

1 bit + 1 bit:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10

On se souvient que 10 binaire vaut 2 en décimal.

Addition en binaire: 5 + 6

5 = 1x4 + 0x2 + 1 => 1 0 1

6 = 1x4 + 1x2 + 0 => 1 1 0

Somme bit à bit: 1 0 1 1

Vérification du résultat:

1x8 + 0x4 + 1x2 + 1 = 11

qui est bien égal à 5 + 6.

Addition en binaire: 5 + 7

5 = 1x4 + 0x2 + 1 => 1 0 1

7 = 1x4 + 1x2 + 1 => 1 1 1

Somme bit à bit: 1 1 0 0

Vérification du résultat:

1x8 + 1x4 + 0x2 + 0 = 12

qui est bien égal à 5 + 7.

ADDITIONNEUR 1 bit + 1 bit:

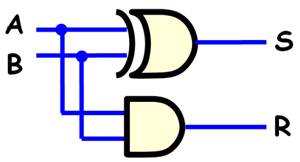
appelé: demi-additionneur

Comment construire le circuit logique qui permettra l'addition en binaire d'un seul bit ?

Table de vérité de l'addition de 1 bit (A) + 1 bit (B):

A	B	Retenue R	Somme S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

On retrouve la table d'addition binaire sous une autre forme, mais c'est la même

Note: on dit table de vérité, car en logique le "1" est assimilé à "vrai" et le "0" à "faux".

Analyse de la table de vérité

La colonne somme correspond à la fonction logique "ou exclusif" et la colonne de la retenue correspond à la fonction logique "et"

Circuit logique

avec une porte OU exclusif

et une porte ET.

S ne sera à 1 que si A ou B est aussi à 1, sans que les deux le soit.

R ne sera à 1 que si A et B sont à 1.

Retenue: addition de 1bit + 1 bit + retenue

Table de vérité de l'addition de 1 bit (A) + 1 bit (B) + retenue (C)

A	B	C	Retenue R	Somme S
0	0	0	0	0
0	1	0	0	1
1	0	0	0	1
1	1	0	1	0
0	0	1	0	1
0	1	1	1	0
1	0	1	1	0
1	1	1	1	1

Toutes les lignes, sauf la dernière, sont simples: c'est la table d'addition ordinaire vu ci-dessus. Exemples: 1 + 0 + 0 = 1 ou 1 + 1 + 0 = 10.

La dernière ligne est nouvelle: 1 + 1 + 1 = 11. On retrouve ce résultat en passant en décimal, car 11 binaire c'est 3 décimal.

Anglais: retenue se dit: Carry (d'où le C pour son symbole)

Observations

On remarque que la somme est un double exclusif. En effet, le C = 1 a pour effet d'inverser l'exclusivité de A et B

S = A B C

Quant a colonne retenue, elle est un peu plus coriace! La seule chose que l'on peut dire à ce stade est que, si A+B provoque une retenue, alors il y a bien retenue finale (R = 1). Voyons ce que l'on peut faire en indiquant les résultats intermédiaire de l'addition A+B, noté R' et S':

A	B	R'	S'	C	R	S
0	0	0	0	0	0	0
0	1	0	1	0	0	1
1	0	0	1	0	0	1
1	1	1	0	0	1	0
0	0	0	0	1	0	1
0	1	0	1	1	1	0
1	0	0	1	1	1	0
1	1	1	0	1	1	1

Notons en chiffres rouges le résultat de notre première remarque: si R' alors R.

Il reste deux R=1 a coder (encadré rouge): R = 1 si S' et C sont à 1.

Nous tenons notre relation logique:

R = R' ou S' et C

Et, nous pouvons concrétiser par le circuit logique

Voir Simplification avec Karnaugh

Circuit logique de l'additionneur

Nous devons réaliser:

S = A B C = S' C

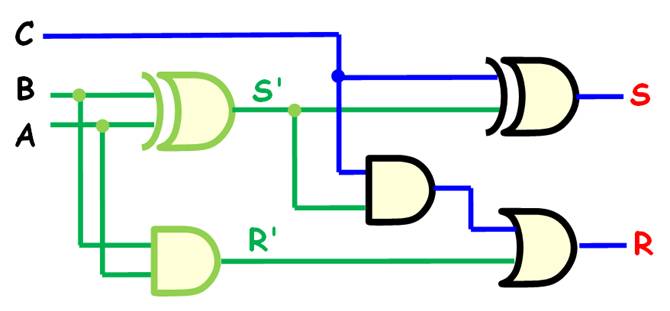
R = R' ou S' et C

Nous voyons que nous avons besoin de R' et S', soit l'additionneur 1 bit dont nous connaissons le circuit (vert).

Auquel, on ajoute le traitement de la retenue (C, circuit en bleu). Pour cela, il nous faut ajouter un ou exclusif entre C et S'; un et entre C et S'; et, un ou entre ce résultat et R'.

Note: sur les schémas logiques, on a pris l'habitude de n'utiliser que des segments horizontaux et verticaux, sans doute pour se préparer au dessin du circuit imprimé qui en sera déduit.

Addition n bits
Pour additionner deux nombres de n bits, il suffit de cascader le circuit que nous venons de définir:
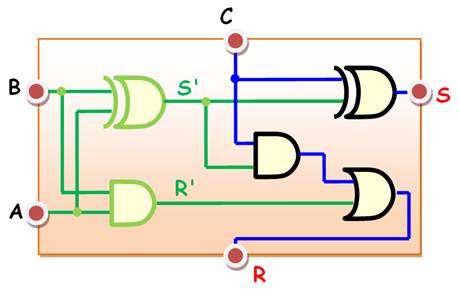
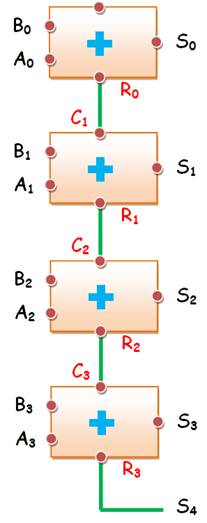
Et cela, autant de fois que de bits dans les nombres à ajouter. Pour ajouter et , composés de quatre bits chacun, il faut quatre circuits montés comme suit: Le résultat est: , sans oublier la dernière retenue en tant que bit de poids forts (chiffre le plus à gauche). Du fait que la retenue se propage de circuits en circuits, le calcul pour de grands nombres peut être long. Pour éviter cet inconvénient, le calcul des retenues est anticipé et la réalisation pratique est un peu plus complexe que celle présentée ci-dessus.