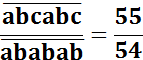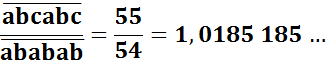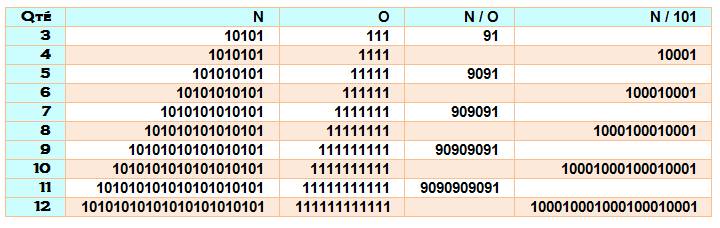
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/02/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	NOMBRES
Débutants Nombres	Divers				Glossaire Nombres
INDEX DicoNombre	Nombre 26	Nombre 37	Nombre 101	Nombre 137
		Sommaire de cette page >>> 101, 10101 … >>> Factorisation

NOMBRES 101 …

Suite alternée de 1 et 0. Seul 101 est premier.

Divisibilité – Exemples

Les suivants sont divisibles par 101, si une quantité paire de 1, et par 111…1 (un repunit) si la quantité de 1 est impaire.

Formules

Une bien jolie devinette

Trouver la valeur des lettres a, b et c.

Solution

101 & 10101 …
Affirmation La suite alternée 10101… forme un nombre qui n'est jamais premier sauf pour 101. Démonstration
L'affirmation est vraie pour les nombres terminés par 0.	Ils sont pairs
Que valent ces nombres lorsqu'ils sont terminés par 1.	101 = 10^2 + 1 10101 = 10^4 + 10^2 + 1 n = 10^2k + …. + 10^2 + 1
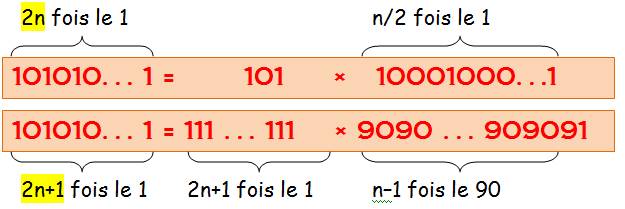
Intuition! Multiplions n par 99 Avec 99 = 10² – 1	(10^2 – 1) (10^2k + …. + 10^2 + 1) = 10^2k+2 + 10^2k – 10^2k + …. + 10^2 – 10^2 – 1 = 10^2k+2 – 1 = (10^k+1 – 1) (10^k+1 + 1)
Observation: les deux facteurs sont plus grands que 100.	Si k = 1 => (10^3 – 1) (10^3 + 1)
Soit une nouvelle expression de la valeur de n.	n = (10^2k+1 – 1) (10^2k+1 + 1) / 99
L'un des deux facteurs est divisible par 99 et le quotient est plus grand que 1. n est le produit de deux facteurs chacun plus grand que 1. CQFD.	n n'est pas premier
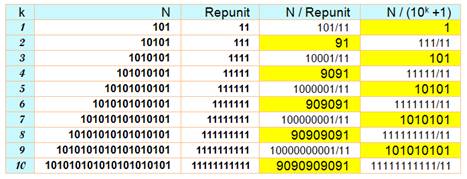
Exemples On se souvient que 111 = 3 x 37	10101 = (10^2+1 – 1) (10^2+1 + 1) / 99 = 999 x 1001 / (9 x 11) = 111 x 91 1010101 = (10^2k+1 – 1) (10^2k+1 + 1) / 99 = 9999 x 10001 / 99 = 101 x 10001

Factorisation et produit (autre méthode de démonstration)
Exemple avec k = 3, k étant la quantité de 1. Facteurs:	N = 10101 = 3 x 7 x 13 x 37 = 91 x 111
Un produit particulier Cette multiplication produit un repunit comportant 2k fois le "1".	11 N = 11 x 10101 = 111 111 = 111 x 10^3 + 111 = 111 (10^3 + 1 )
D'une manière générale:	N = 101k…01 11 N = 112k …1 = 11k …1 (10^k + 1) = U . V
Si k est pair, le repunit U est formé d'un nombre pair de 1, ce qui est suffisant pour être divisible par 11.		k pair => 11 U = 11k …1 k impair => 11 U = 11k …1
Si k est impair, c'est l'inverse. Toujours en sommant les chiffres de rang pair et ceux de rang impair; la différence est nulle.		k impair => 11 V = 10k …1 k pair => 11 V = 10k …1
Conclusion: dans tous les cas:		11 U ou V pas les deux à la fois.
Si c'est U qui est divisible par 11: U = 11 u Si c'est V qui est divisible par 11: V = 11 v		11 N = 11 . u . V => N = u. V 11 N = 11 . U . v => N = U. v
Dans tous les cas:	N est divisible par U ou par V.
Cas où k = 2:	N = 101 U = 11 V = 10² + 1 = 101 V = N or on sait que 101 est premier.
Autres cas:	N est divisible ou par le repunit U ou par V = 10^k + 1), deux valeurs qui différent de 1 et de N. N est donc composé.
Les premières valeurs pour vérification:

Devinette – Solution

Trouver la valeur des lettres a, b et c. On rappelle que la barre en haut signifie qu'il s'agit d'un nombre, ici, à six chiffres.

Solution

Magique

La fraction trouvée correspond pilepoil à la fraction littérale.

a = 1, b = 8 et c = 5

Retour / Magie / Cryptarithme

Suite	Nombre 101
Voir	Premier Repunits Nombres ondulants Nombres typiques par leur forme Nombre 101 Repdigit
DicoNombre	Nombre 1, 0185 185 …
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Nombre/Nb101.htm