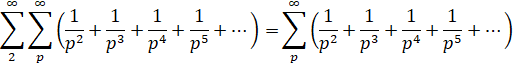|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
Citation
|
On n’a qu’à jeter les yeux sur les tables des nombres premiers, que
quelques personnes se sont donné la peine de continuer au-delà de cent mille :
et on s’apercevra d’abord qu’il n’y règne aucun ordre ni règle. |
Voir Pensées et Humour
|
PROPRIÉTÉS des NOMBRES PREMIERS Quelques propriétés
typiques des nombres premiers. |
|
Pouvez-vous
trouver tous les nombres premiers p tels
que 5p + 1 soit un carré? |
|
PROPRIÉTÉS fondamentales |
|
|
Explications >>> |
|
|
|
||
|
0 |
|
|
|
1 |
(facilite l’énoncé
de certaines propriétés) |
|
|
2 |
|
|
|
5 |
|
|
|
3, 5, 7 |
|
|
|
1, 3, 7, 9 |
|
|
|
4 |
|
|
|
6 |
|
|
|
1, 9 |
|
|
|
|
|
|
Caractérisation du nombre premier |
|
|
|
|
|
Valeur |
|
Hadamard et La Vallée-Poussin en 1896
|
|
Parité et puissances |
|
En effet: le produit de deux nombres premiers
distincts ne peut pas être factorisé comme produit de deux facteurs
identiques. Voir P x P'
non C²
Conjecture
de Goldbach
Fermat, démontré
par Euler |
|
Ce
qui veut dire aussi que pour n > 10: il existe plus de premiers entre 1 et n
qu'entre n et 2n. Postulat
de Bertrand (1845) démontré par Tchebychev (1852) Démonstrations
plus simples par Ramanujan puis par
Paul Erdös (1932) Voir Belle
application avec les factorielles / Nombres premiers de
Ramanujan
Entre n² et (n + 1)², il existe toujours
un nombre premier; ils sont même
d'autant plus nombreux que n est grand. Conjecture de
Legendre. Démontré:
il existe un premier entre n23/42
– n
|
|
Voir Liste de ces nombres |
|
1/2+1/3+1/5+1/7+1/11+… tend vers l'infini. Euler,
démontré en 1737 - Voir Série harmonique
1/3 + 1/5
+ 1/5 + 1/7 + 1/11 + 1/13 + 1/17 + 1/19 + 1/29 + 1/31 + ... = 1,902...
p
indiquant somme sur tous les nombres premiers existant de 2 à l'infini |
|
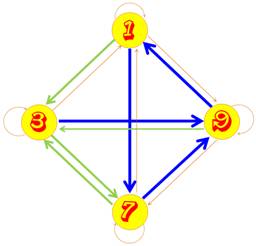
Préférence des nombres premiers Un nombre premier "n'aime" pas
être suivi par un autre ayant la même unité. |
|
|
Propriété découverte et démontrée par
Kannan Soundararajan et Robert Lemke Oliver (Stanford University) – 2016. Anglais: last digits
of nearby primes have ‘anti-sameness’ bias.
Un nombre se terminant par 1 aura deux fois
plus de chances d’être suivi par un premier se terminant par 2 plutôt que par
1. De même, un premier se terminant par 2 préfère être suivi par un premier
se terminant par 1. Exemple pour les premiers de 1000 à 1200
L'amplitude des oscillations témoignent de
la répulsion entre premiers de même unité. En rouge, les premiers amis
d'unités.
Nos deux mathématiciens ont exploité
un modèle de production statistique des nombres premiers basé sur le fait
que: La densité
de nombres premiers autour d'un nombre quelconque est inversement
proportionnelle au nombre de chiffres pour écrire le nombre. En 1936, Harald Cramer mit au point avec
succès un tel modèle qui fut perfectionné ultérieurement. Cependant un tel
modèle ne créé aucune préférence pour le choix de l'unité.
Conjecture émise par G. H. Hardy and J. E. Littlewood
en 1923 qui donne une estimation de la quantité de fois qu'une constellation de premiers se produit, généralisation
de la conjecture des premiers jumeaux. Les deux mathématiciens y ont trouvé un air
de similitude, le même biais. |
|
|
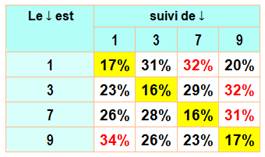
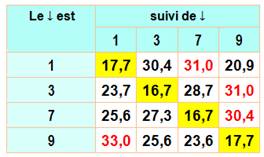
Exemples selon mes calculs. 17% (ou 17,7%) des
nombres premiers terminés par 1 sont suivis par un autre premier terminé lui
aussi par 1. À peu près la même chose pour 3, 7 et 9 (diagonale en jaune). Conclusion:
moins de 20¨% des premiers sont suivis
d'un premier de même unité. Sur ce graphique, en bleu les
préférence pour chaque chiffre-unité.
|
Pour n de 7 à 10 millions
Pour n de 1 à 100 millions
|
Source: Mathematicians
Discover Prime Conspiracy – Erica Klarreich – 13/04/2016 – Quanta Magazine
|
concernant les nombres premiers |
|
|
|
|
Non résolus en 2017 |
|
|
|
En nombre infini ? |
|
|
|
? |
|
|
|
En nombre infini ? |
|
|
|
Vrai ? |
|
|
|
En nombre infini ? |
|
|
|
? |
|
|
|
Longueur infinie ? |
|
|
|
En nombre infini ? |
|
|
|
En nombre infini ? |
|
|
|
En nombre infini ? |
|
|
|
En nombre infini ? |
|
|
|
En nombre infini ? |
|
|
|
En nombre infini ? |
|
|
|
En nombre infini ? |
|
|
|
Toujours ? |
|
|
|
||
|
|
|||
|
Affirmation
Démonstration par induction |
|||
|
C'est vrai. |
3
< 22 |
||
|
L'est-elle pour n + 1? Effectivement nous retrouvons bien la
formule avec n remplacé par n+1. |
pk
< 2k pk+1
< 2k+1 ? |
||
|
|
pk
et 2pk |
||
|
|
pk+1
< 2pk |
||
|
|
pk+1
< 2pk < 2 x 2k = 2k+1 |
||
|
Exemples |
5
< 23 = 8 7
< 24 = 16 11 < 25 = 32 |
||
|
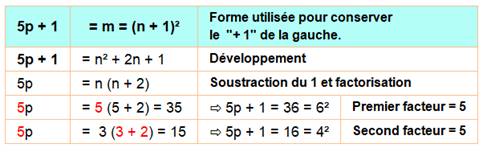
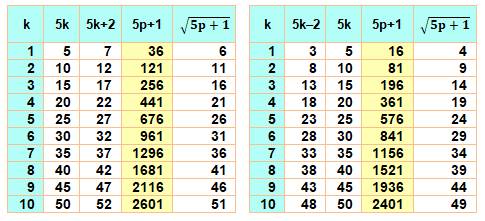
Question Pouvez-vous
trouver tous les nombres premiers p tels
que 5p + 1 soit un carré? Réponse
Généralisation En
fait, toutes les valeurs en Tableau
Bilan Grand
cas pour simplement avoir explicité le calcul de 5p + 1 = (5k Ex:
sur la première ligne 5k + 1 = 6 et 5k – 1 = 4. |
Merci à Jean-Dany D.
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()