|
||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES ONDULANTS Nombres du type
121212121212… Leurs propriétés. Quels sont ceux qui sont premiers, une
puissance ? |
Anglais: Undulating
numbers
|
|
|
|
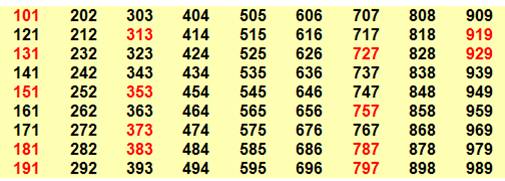
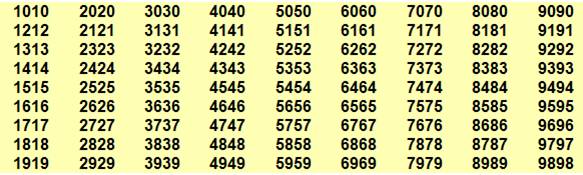
Exemples: 121, 1212, 12121, 121212, … Nombres ondulants à trois chiffres (81)
En rouge, les 15 ondulants premiers. Nombres ondulants à quatre chiffres (81)
Aucun ondulants premiers à quatre chiffres.
Ils sont 90 si l'on admet les cas ou a = b (comme
111 ou 999). |
|
|
|
|
|
Voir
Tables des nombres ondulants en
01 avec facteurs et divisibilités |
|
|
|
|
|
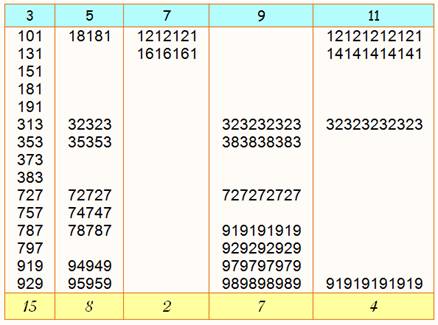
1212121 ( 7 chiffres) est premier.
Le plus petit. 12121212121 (11 chiffres est
premier. 12121212…21 (43 chiffres est
premier) Quantité de chiffres de ces nombres
premiers: [7, 11, 43, 139, 627, 1399, 1597, 1979] Voir Table
des nombres premiers ondulants |
|
|
|
|
|
121 = 11² 484 = 22² 676 = 26² 69 696 = 264²
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Livres |
|
|
Cette page |
![]()