NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/06/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	NUMÉRATION
Débutants Binaire	BINAIRE			Glossaire Général
INDEX Numération	Introduction	Nombres négatifs	Conversion	Table 0 à 512
	Code Gray	Informatique	Dualité	Amusement
	Logique de Boole	Analog. / Numér.		Magie
		Sommaire de cette page >>> En pratique, comment faire ? >>> Première idée >>> La bonne idée >>> Vision circulaire >>> Comprendre l'astuce >>> Opérations

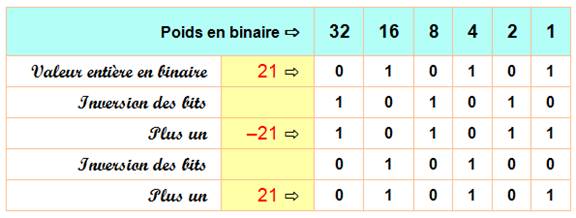
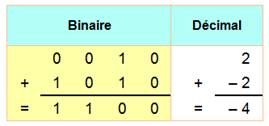
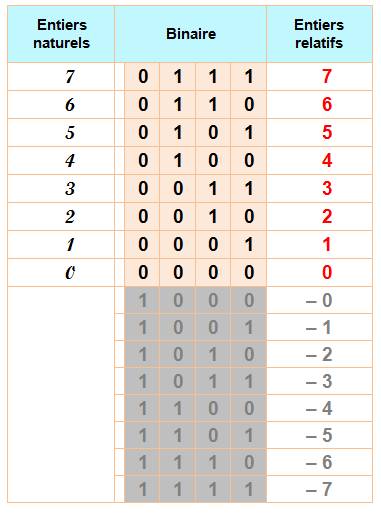
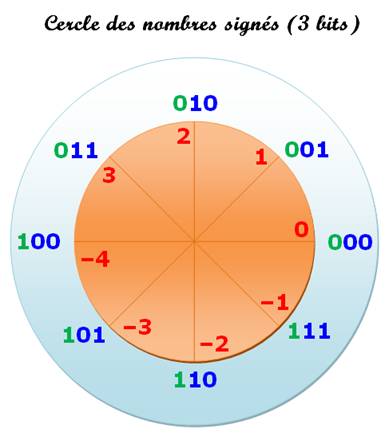
NOMBRES NÉGATIFS

en BINAIRES

Les nombres négatifs sont codés de façon que les opérations classiques puisent être effectuées normalement. Autrement dit, 2 + (-2) doit bien donner 0 pour somme.

En pratique, comment faire?

Les nombres positifs sont codés normalement; tandis que les nombres négatifs sont codés selon leur complément à deux. En pratique, voici ce qu'il faut faire avec 21 par exemple: De positif à négatif: coder, inverser et ajouter 1. Pour passer du négatif au positif: inverser et ajouter 1. En fait, le bit de poids 32 ne joue plus ce rôle "pesant". C'est désormais le bit de signe. Voir Codage binaire pour traitement numérique

Première idée
Ce qui semble le plus naturel serait de prendre les nombres binaires en valeur absolue et d'ajouter en tête un bit de signe: 0 pour positif et 1 pour négatif. Essayons de calculer 2 + (–2) = 0 Ce n'est pas ce que nous voulions: –4 au lieu de 0! Remarquez que nous avons deux fois le zéro, en plus et en moins. inadmissible. Il faut revoir notre copie.

La bonne idée

L'idée est simple et elle marche! Au lieu de prendre les en dessous, prenons-les au-dessus. Comment? En poursuivant le compte avec des entiers naturels. Les entiers naturels et leur code binaire sont prolongés: 0, 1, 2 … 7, 8, 9, …14 et 15. Nous décrétons que le premier bit à gauche est le bit de signe et que les codes binaires des nombres 8 à 15, dont le premier bit est à 1, sont le codage de nombres négatifs. Lesquels? Le code du complément du nombre entier à 16. Ainsi, le 15 naturel de code 1111 devient la valeur négative du nombre: 16 – 15 = 1, soit: –1. Le bit de poids 16 n'existe pas. C'est lui l'astuce. En effet 2 + (–2) devient 0010 + 1110 = 1 0000 avec le premier 1 qui tombe dans le vide. on l'oublie. Ainsi: 0010 + 1110 = 0000. L'opération est juste. Le fait de complémenter à la puissance de 2 correspondante à un bit de plus est appelé: complément à 2. Deux étant la base de numération.

Vision circulaire
Les nombres positifs et négatifs sont enroulés sur le cercle. Les nombres sont disposés symétriquement par rapport au diamètre horizontal. Avec trois bits nous comptons de – 4 à + 3. Remarquez que 2 + (–2) = 0 se comprend également en binaire sur 3 bits: 010 + 110 = 1 000 soit un bit qui tombe dans le vide (Nous n'en connaissons que trois), soit 010 + 110 = 000. Cette remarque explique le vocable de complément à 2 (ou plutôt, à une puissance de 2). Coté pratique, comment passez de 2 à –2 ? C'est particulièrement simple. 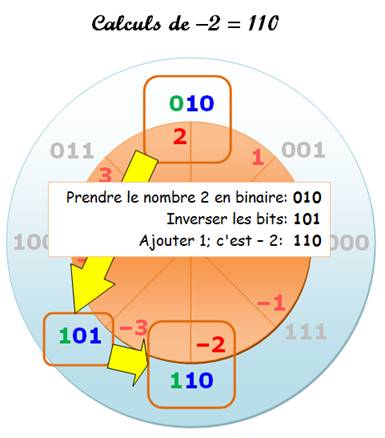Il suffit d'ajouter 1 aux bits inversés: 2 => 010 Inversion: 101 (ou complément à 1) Plus1: 110 (ou complément à 2)

Cerise sur le gâteau

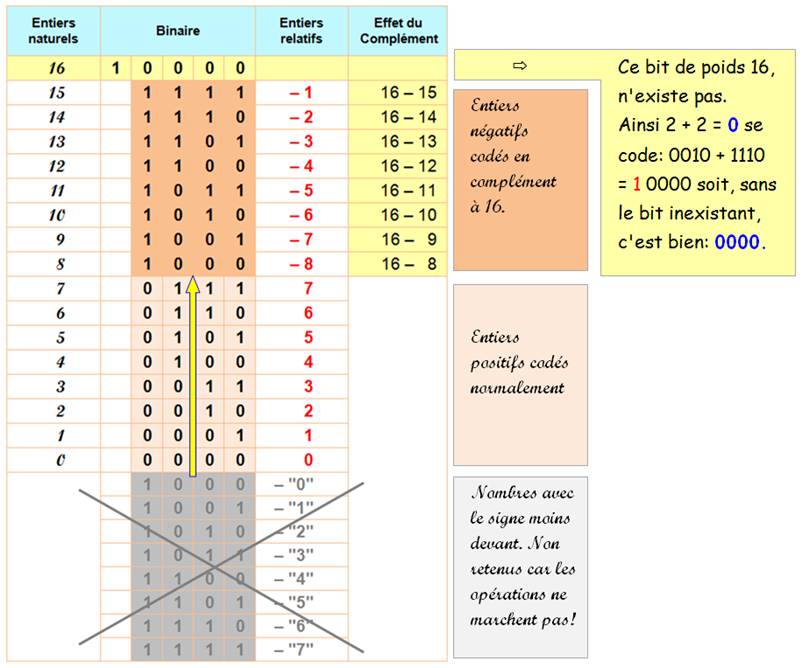
Pour passer d'un format à 4 bits à un format à 8 bits (par exemple), il suffit de prendre les nombres binaires à 4 bits et de remplir tous les nouveaux bits à gauche par le bit de signe.

0100 = 0000 0100 (4 en décimal)

1100 = 1111 1100 (–4 en décimal)

En effet: 1111 1100 => 0000 0011 + 1 = 0000 0100.

Comprendre l'astuce

Astuce du complément L'astuce du complément à 2 pour représenter les nombres négatifs rend faisable le calcul en binaire. On peut en avoir une idée avec cet exemple, classique en calcul mental: 120 – 99 = 120 – (100 – 1) = 120 – 100 + 1 = 20 + 1 = 21 Base 10 En base 10, pour signifier –7, on peut aussi dire –10 + 3. En fait, 3 est le complément à 10 (la base de numération) de 7. On note qu'il faut mentionner d'une manière ou d'une autre le –10. On pourrait noter par exemple: 07, le nombre 7 positif, et 13, le nombre 7 négatif => 7 = 10 – 3 = 10 – (10 – 7) Un autre exemple: 099, le nombre 99 positif, et 101, le nombre 99 négatif => 99 = 100 – (100 – 99) Le premier chiffre en vert témoigne du signe de l'opération. Base 2 En binaire on utilise le complément à 2. Selon le même principe qu'en décimal: N = 2^2 – (2^2 – N)

Suite	Nombres binaires et traitement numérique Langage des ordinateurs Junior Diaporama Nombres en binaire flottant
Voir	Bases de numération Base 20 Carré de Dürer en binaire Nombres – Glossaire Dualité Trigramme Conversion Code Gray Additionneur Nombres binaires et triangle de Pascal Suite binaire dorée Langage binaire des ordinateurs Table 1 à 10 en binaire
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Numerati/BINAIRE/Introduc.htm