|
||||||||||||||||||||||||||||||||||||||||||
![]()
|
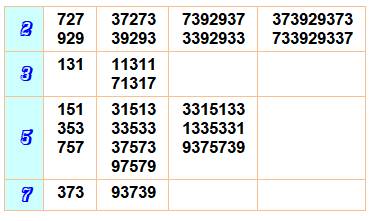
Nombres PPP Premiers Palindrome en Pyramide Nombre premier palindrome
tel qu'en effaçant les chiffres de chaque côté, il demeure premier. Il est résistant à la fois à droite et à gauche avec le même
chiffre. |
|
|
|||
|
Avec le
plus petit nombre premier 2, construire un nombre premier palindrome dont 2
est le centre. |
|||
|
Avec deux
étages |
2 727 |
2 929 |
|
|
Avec
trois étages |
2 727 37273 Fin |
2 929 39293 |
|
|
Avec
quatre étages |
2 929 39293 7392937 |
2 929 39293 3392933 |
|
|
Continuez
le procédé en créant un nouveau nombre premier palindrome avec 929 au centre.
Etc. Maximum
atteint avec quatre itérations et deux possibilités. |
2 929 39293 7392937 373929373 Fin |
2 929 39293 3392933 733929337 Fin |
|
|
|
||
|
|
Commentaires Deux procédures et le programme principal. La première procédure fournit la liste
L des nombres palindromes formés du nombre n et d'un chiffre accolé de chaque
côté. Seuls 1, 3, 7, 9 sont possibles. La formule tient compte de la quantité de
chiffres q du nombre semence. La deuxième procédure retient les seuls
nombres premiers dans la liste B à partir de la liste A des palindromes
formés à partir de n. Le programme principal identifie les
23 nombres premiers pyramides et les place dans la liste E. La semence initiale sont les quatre nombres
premiers à un chiffre: 2, 3, 5, 7. On pratique cinq itérations (j) de formation des
palindromes. On peut faire plus pour s'assurer de l'extinction de la
production de premiers. La boucle suivante en i explore tous les nombres
présents considérés comme semence. Pour chacun, on recherche les nouveaux
premiers avec un chiffre de plus sur chaque côté (emploi des procédures en
cascade). En fin de programme, on demande l'impression de
l'ensemble E en utilisant les accolades qui supprime les redondances et range
les nombres par ordre croissant. On pourrait améliorer le programme pour le rendre
plus "propre" en ajoutant à E que les nouveaux premiers venus. En bleu, le résultat de
l'exécution du programme. |
|
Voir Programmation – Index
|
Exemple:
avec la semence 2, le nombre 30203 est premier, de même que 903020309, etc. |
Voir
exemples en Référence Honacker / Caldwell
ci-dessous
![]()
|
Voir |
|
|
Voisins |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
![]()