|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DOUBLE-SIX aux dés ou Problème du chevalier Méré (1654) Obtenir un double six une
fois sur deux ! Solution de Pascal qu'il
a pris soin de vérifier auprès de Fermat |
|
|
|||
|
Un
jet de deux dés |
|||
|
|
1/6 x 1/6 = 1 – 1/36 = |
1/36 35/36 |
|
|
Deux
jets de deux dés |
|||
|
|
Calcul direct 35 /36 x 35/36 1 – (35/36)² |
= difficile = (35/36)² = 5, 4% |
|
|
N jets de deux dés |
|||
|
|
Calcul direct 35 /36 x 35/36 x … |
= difficile = (35/36)N = 1 – (35/36)N |
|
|
Le problème sur la
probabilité du double six |
|
||
|
|
Calcul
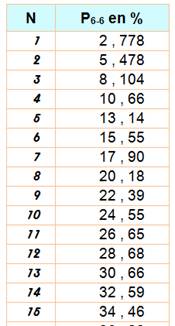
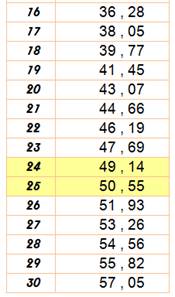
pour les valeurs de N
Exemple: Si je lance 15 fois deux dés, j'ai 34,46% de chance d'obtenir un
double-six. |
||
|
|
||
|
|
P = 1 – (1 – p) N |
|
|
Vérification du résultat de
Pascal |
|
||
|
|
1 – (1 – p) N |
= 1/2 |
|
|
|
N . log(1 – p) |
= – log 2 |
|
|
|
N |
= – log 2 / log(1
– p) |
|
|
|
log(1 –
p) |
= – p – p2/2 – p3/3 – … |
|
|
|
p |
= 1/36 |
|
|
|
log(1 –
1/36) |
= 0,0281708… |
|
|
|
log 2 |
= 0,693147… |
|
|
|
N |
= 24,60… |
|
|
|
|||
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Probabil/DesDoSix.htm |
![]()