jeu de dés, introduction

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 17/04/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths et hasard
Débutants Statistiques	PROBABILITÉS & Statistiques				Glossaire Probabilités
INDEX Grands nombres Dénombrement	Jeu de dés		Deux dés	Double Six
	Dénombrement		Trois dés	Probabilités et Dés
	Numérotation		Trois dés et une urne	Table 1 à 6 dés
			K chiffres identiques	Proba. mêmes chiffres
		Sommaire de cette page >>> Jeux de dés >>> Devinettes >>> Six dés >>> 0,666 et les dés

Le jeu de DÉS

Un dé est un cube dont les six faces sont marquées de points de 1 à 6.

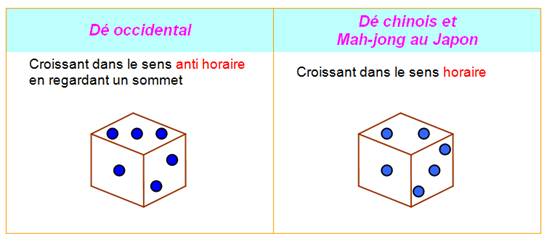
La somme des points des faces opposées est égale à 7.

Avec deux dés, la somme 7 est la plus probable (16,6% = 1/6).

Il existe deux sortes de dés selon l'orientation du marquage des points.

Anglais: dice game >>>

Le jeu de dé

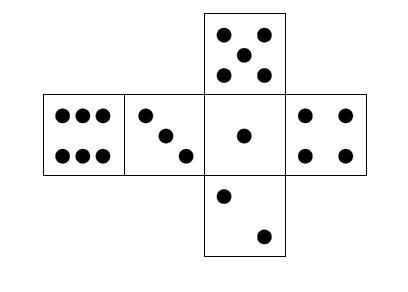
Développement du dé

Remarquez que les sommes égales à 7 = 6 + 1 = 3 + 4 = 5 + 2

La somme des points: 1 + 2 + 3 + 4 + 5 + 6 = 6 x 7 / 2 = 21

Voir Amusement (tour de magie) avec deux dés

Deux types de dés

Il reste deux possibilités pour le dé, l'une est l'image de l'autre dans un miroir. Dans les deux cas les faces 1, 2 et 3 se touchent par un sommet du cube.

Voir Possibilité de numérotation du dé

Anglais: Dice game

DEVINETTES basée sur la propriété des dés
Principe	Exemple	Théorie
Lancer 3 dés	2, 4, 6	*a, b, c*
Additionner	12	*S1 = a + b + c*
Choisir un dé	2	a
Ajouter les points de la face cachée	12 + 5 = 17	*S2 = 7 – a + a + b + c* *= b + c + 7* " a " disparaît de la somme
Relancer ce dé (les autres restent sur le tapis)	5	d
Ajouter la nouvelle valeur	17 + 5 = 22	*S3 = b + c + d + 7*
Le magicien, en voyant pour la première fois les dés, annonce que le total précédant était 22	4 + 6 + 5 + 7 = 22	*S3 = somme des dés* *+ 7*

Martin Gardner (1914-2010)

Lancer 3 dés	2, 4, 6	*a, b, c*
Doubler la valeur du premier dé	4	2a
Ajouter 5	9	*2a + 5*
Multiplier par 5	45	*5(2a + 5) = 10a +25*
Ajouter le second	49	*10a + b + 25*
Multiplier par 10	490	*100a + 10b + 250*
Ajouter le troisième	496	*100a + 10b + c + 250*
On donne la somme au magicien qui donne la valeur des 3 dès sans les voir	496 – 250 = 246	abc_{base 10} + 250

Henri Ernest Dudeney (1857-1930)

SIX DÉS

Question

On lance 6 dés (non pipés !) en un seul jet.

La somme des points sur les dés donne un nombre de 6 à 36, soit 31 valeurs.

Nous souhaitons connaître la probabilité de tirage de chacun des 31 numéros.

Réponse

Dénombrement

Confirmons le total des cas possibles : 46 656

Le premier dé offre 6 possibilités;

Pour chacune de ces possibilité, le deuxième dé peut prendre l'une des six valeurs, soit un total de 6 x 6 = 36 possibilités avec ces deux dés;

Pour chacune de ces 36 possibilités, le troisième dé peut prendre une des six valeurs, soit 36 x 6 = 216 possibilités, ou exprimées autrement: 6 x 6 x 6 = 6³;

Avec 6 dés, il y a 6⁶ = 46 566 possibilités.

Voir Dénombrement p-liste

0, 666 … et probabilités aux dés

0,666 =	4 x 1/6	N'est pas	La probabilité d'obtenir au moins un six en 4 lancers de dé.
0,518 =	1 – (5/6)⁴	Est
0,666 =	24 x 1/36	N'est pas	La probabilité d'obtenir un double six en 24 lancers de dé.
0,491 =	1 – (35/36)²⁴	Est	La probabilité d'obtenir un double six en 24 lancers de dé.

La bonne méthode consiste à calculer les cas ou nous n'avons pas de double six.

Cas de un seul lancer de dé: j'ai toujours un double-six (1) sauf tous les cas où je l'ai pas (5 fois sur 6), ce qui donne la probabilité d'avoir un double-six avec un dé: 1 – 5/6 = 1/6.
Avec deux lancers: 1 – (5/6)² = 11/36 = 0,305… et non pas 2/6 = 0,333…

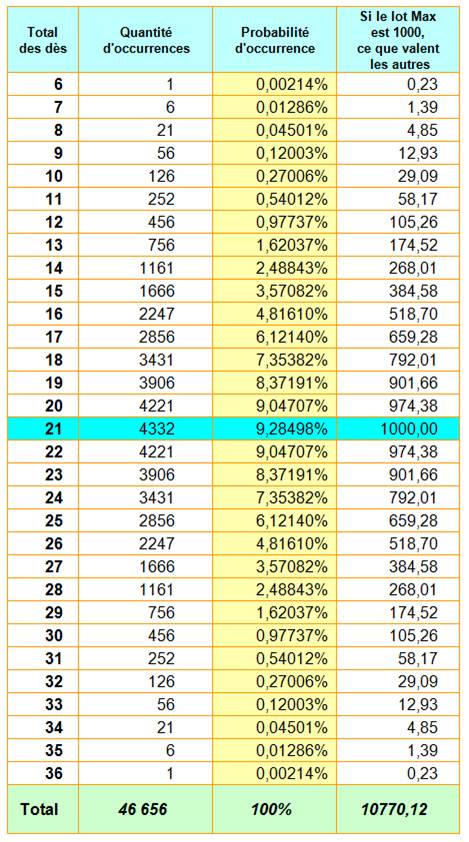
Suite Dés et probabilités

Suite	421 Craps Trois dés Paire de dés Dés de Cardano Loterie à trois dés Numérotation possibles de 1 à 6 Calendrier à deux dés
Voir	Dénombrement Échecs Jeux – Index Jeux de hasard (loto, tiercé …) Pentominos Probabilités Trois pièces
DicoNombre	Nombre 6
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Probabil/DesJeu.htm