NOMBRES - Curiosités, théorie et usages Accueil / Dictionnaire / Rubriques / Index / Atlas / Références / Nouveautés ORIENTATION GÉNÉRALE  - M'écrire - Édition du: 22/12/2012
Débutants Types de Nombres	TYPES NOMBRES / TYPES	Glossaire Nombres
	APPROCHE IMAGÉE
Sommaire de cette page >>> APPROCHE Imagée >>> SQUASH et TENNIS >>> Les nombres ENTIERS et RELATIFS >>> Les nombres ENTIERS NATURELS >>> Les nombres ENTIERS RELATIFS >>> Les nombres RATIONNELS >>> Les nombres IRRATIONNELS >>> Les nombres RÉELS >>> Les nombres COMPLEXES

Retour vers Index de ces pages

---

Les différents types de NOMBRES Nous allons essayer de voir pourquoi les mathématiciens ont été amenés à créer divers types de nombres. On va découvrir que les différents types de nombres répondent à des besoins précis: les résultats des opérations
Si je prends une balle et que je la lance, elle retombe dans ma cour ou dans celle d'à côté.	Si je prends deux nombres et une opération: le résultat est un nombre de même type ou…d'un autre type

APPROCHE – Les deux mains

Mettez vos deux mains à plat sur une table. Observez! Elles sont vraiment différentes ! On ne peut pas passer de l'une à l'autre facilement. Elles ne se superposent pas. En retournant l'une des mains, elles se retrouvent paume à paume ou dos à dos, mais jamais l'une semblable à l'autre. Avec des gants, peut-être y arriverait-on ? Oui, en les retournant "dedans-dehors" chacun des doigts d'un gant. Alors là, nous avons une petite idée de ce qu'il faut. En fait, la vraie solution passe par une quatrième dimension. Un autre monde. Le recours à un autre monde extérieur pour travailler et trouver une solution dans notre monde est un phénomène classique en mathématiques.

Squash et tennis
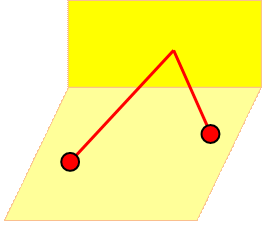
Squash Les joueurs jouent en envoyant une balle qui rebondit sur un mur. Un camp. Toutes les balles reviennent dans ce camp. Quelle que soit la partie, les balles reviennent toujours dans le terrain de jeu. Elles ne peuvent pas en sortir.	Tennis Les joueurs se font face et jouent l'un contre l'autre. Deux camps. Les balles passent d'un camp à l'autre. Pour jouer au tennis, il faut deux camps. Et, ayant mis en place le deuxième camp, les balles sont dans l'un ou l'autre mais pas à l'extérieur (oublions les sorties de balles).

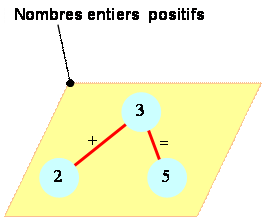
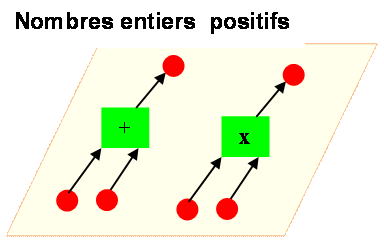
Les entiers et les relatifs
Entiers Avec les nombres entiers, je joue à les additionner: 2 + 3 = 5 Un camp: les entiers positifs. Toutes les additions donnent une somme qui est un entier positif. On reste dans le même camp. Quelle que soit l'addition de deux nombres entiers, la somme est un nombre entier. On ne sort pas du camp (de l'ensemble) des entiers. L'ensemble des entiers est clos pour l'addition. C'est un invariant pour l'addition.	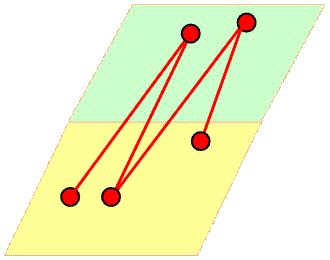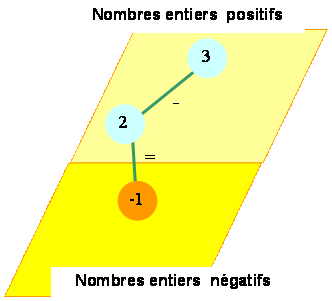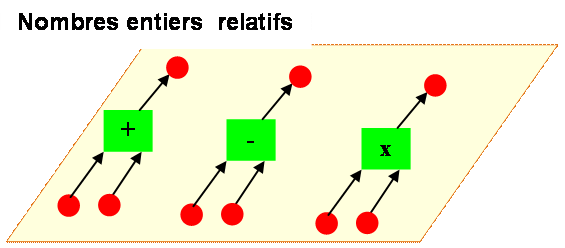Relatifs Avec les nombres entiers, je joue à les additionner et à les soustraire: 2 + 3 = 5 2 – 3 = –1 Deux camps: les entiers positifs et les entiers négatifs. Toutes les additions et soustractions donnent soit des entiers positifs, soit des entiers négatifs. On est dans un camp ou l'autre. Pour jouer avec la soustraction, il faut introduire les nombres entiers négatifs. Mais ayant mis en place ce deuxième camp, les résultats sont dans l'un ou l'autre mais pas à l'extérieur. On ne sort pas du camp combiné des entiers positifs ou négatifs.

LES NOMBRES ENTIERS NATURELS

L'ensemble des entiers naturels est le plus simple. Celui qui sert à compter les choses dans la nature: les moutons, mais aussi … les cailloux qui se dit calculus en latin. · D'où le terme calcul pour compter. · Et celui de calculs dans les reins. Ce sont les nombres sans virgule, sans décimales. Ils n'ont pas de signe; ils sont toujours positifs. Ils ont la propriété de récurrence: passage d'un nombre au suivant en ajoutant 1. Notion qui semble banale, Mais importante dans la théorie des nombres. NOMBRES ENTIERS NATURELS: Ensemble invariant pour ADDITION & MULTIPLICATION Pour ces deux opérations, tous les résultats donnent un nombre entiers naturel.

LES NOMBRES ENTIERS RELATIFS

L'ensemble des entiers relatifs ne complique pas beaucoup les choses pour nous aujourd'hui. On comprend rapidement leur intérêt, en particulier en comptabilité: si je dois de l'argent, c'est, en quelque sorte, de l'argent négatif. Sa compréhension et son acceptation ont été plus problématiques pour les anciens: Comment admettre que, ayant 2 moutons, j'en retire 3, il m'en reste …? Impossible ! Les nombres entiers relatifs sont ceux qui ont un signe devant: En général le signe plus n'est pas indiqué, il est sous-entendu; Par contre, le signe moins est toujours indiqué. Amusant: les comptables notent les nombres négatifs en les mettant entre parenthèses (le signe moins n'est pas assez visible pour eux). Les nombres entiers relatifs sont donc composés: des nombres entiers positifs, des nombres entiers négatifs, et d'un individu fortement nécessaire au milieu, qui est le Zéro. Les nombres entiers naturels (ou positifs) forment une partie de l'ensemble des entiers relatifs. 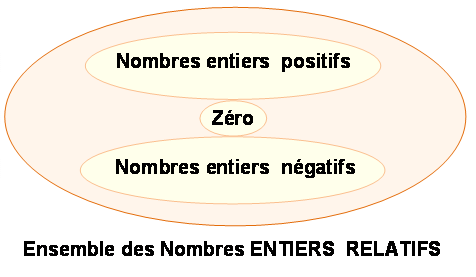NOMBRES ENTIERS RELATIFS: Ensemble invariant pour ADDITION, SOUSTRACTION & MULTIPLICATION Pour ces trois opérations, tous les résultats donnent un nombre entier relatif.

Voir Introduction aux nombre négatifs

LES NOMBRES RATIONNELS
Un nouveau territoire On a bien vu que parmi les quatre opérations classiques, il manque encore la division Eh bien, Oui! Vous le savez, la division de deux nombres entiers ne donne pas forcément un nombre entier. Avec la division, on sort du territoire des entiers relatifs. On l'agrandit avec les nombres fractionnaires, dit aussi rationnels. La division Notation de la division: a = p / q. Quelles sont les valeurs prises par a ? Colonne au centre Notons qu'un nombre illimité de zéro après la virgule ne change pas le nombre: colonne de droite
un nombre entier.	4 / 2 = 2	4 / 2 = 2,000…
un nombre avec une quantité de décimales limitée.	3 / 2 = 1,5	3 / 2 = 1,5000…
un nombre avec des décimales qui se répètent (décimales périodiques).	1 / 3 = 0,333… 1 / 11 = 0,0909…	1 / 3 = 0,333… 1 / 11 = 0,0909…
un nombre avec des décimales qui se répètent à partir d'un certain rang.	1 / 6 = 0,1666…	1 / 6 = 0,1666…

Conclusion

Le résultat de la division de deux nombres entiers

est toujours un nombre avec des décimales périodiques,

au moins à partir d'un certain rang.

Ce sont les nombres rationnels, ou fractionnaires.

Rationnel évoque la ration, la portion d'un gâteau à partager.

Réciproque

Si l'écriture décimale d'un nombre

est un nombre avec des décimales périodiques,

au moins à partir d'un certain rang,

alors, c'est un nombre rationnel.

Rationnels

Les nombres rationnels sont composés:

des nombres entiers relatifs, et

des nombres avec virgules ou nombres décimaux.

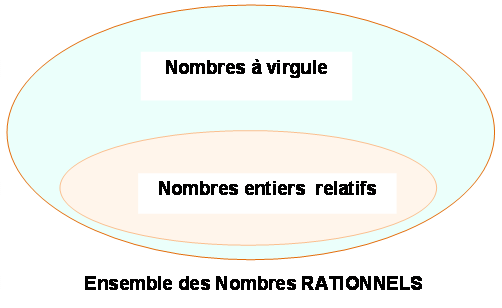
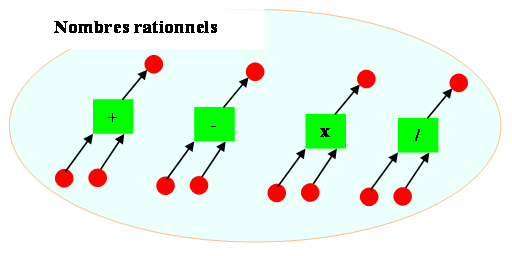
Les nombres entiers relatifs forment une partie de l'ensemble des nombres rationnels.

NOMBRES RATIONNELS

Ensemble invariant pour:

ADDITION, SOUSTRACTION,

MULTIPLICATION & DIVISION

Pour ces quatre opérations, tous les résultats

donnent un nombre rationnel.

LES NOMBRES IRRATIONNELS

Une suite ? Ah, non! Maintenant, on dispose des nombres pour effectuer les quatre opérations. C'est fini ? Non ! C'est sans compter avec les ressources des mathématiques. Et la racine carrée, vous y avez pensé à la racine carrée ? Et les nombres à décimales qui ne répètent pas ? Curieusement, on va trouver une relation entre les deux notions … Racine carrée Soit le carré de côté unité. Sa diagonale mesure 2. Cette valeur résulte de la relation de Pythagore dans les triangles rectangles: d² = 1² + 1² = 2 d = 2 d = 1,414213562… C'est une équation du 2^e degré: x² - 2 = 0 ou x² = 2. On constate, en tout cas, que le résultat est un nombre à décimales non répétitives.

Les nombres irrationnels

Nombres dont les décimales ne se répètent pas.
Ils ne résultent pas de la division de deux entiers

Exemples

0,1234567891011121314… 0,10100100010000100000… 3,141592654…. 1,58976421358…

Suite des nombres Suite avec un zéro de plus Constante PI Totalement au hasard

Les nombres irrationnels forment un monde nouveau.

La racine carrée d'un nombre est:

soit rationnelle, si le nombre est déjà un carré

soit irrationnelle, dans tous les autres cas

LES NOMBRES RÉELS
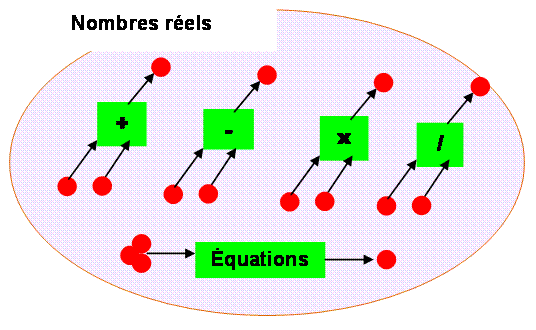
Ensemble complet Les nombres réels sont composés: des nombres rationnels, et des nombres irrationnels. Les nombres réels sont solutions des équations du 2^e degré. Et aussi des équations de degré quelconque. NOMBRES RÉELS Ensemble invariant pour: ADDITION, SOUSTRACTION, MULTIPLICATION, DIVISION & ÉQUATIONS

LES NOMBRES COMPLEXES

Ça continue … À la vérité, les équations sont plus capricieuses que cela. Leurs solutions (racines) sont: des nombres réels, ou des nombres complexes. Les solutions "réelles" n'existent pas tout le temps. Les solutions "complexes" existent toujours. Et, même plus: il y autant de racines, réelles ou complexes, que le degré de l'équation. C'est l'intérêt de l'introduction des nombres complexes: On sait toujours donner les racines des équations. Enfin, presque… Ça se complique à partit du degré 5. Laissons ces aspects un peu trapus pour plus tard…

---

Suite	Inventaire des types de nombres Types de nombres – Index Découverte des nombres Structure algébriques – Débutants
Voir	Calcul mental – Index Carré magique débutant Ensemble - Glossaire Nombre - Glossaire Nombre et anglais Panorama Rubriques débutants Théorie des nombres
Nombres	Liste des nombre de 0 à l'infini et de leurs propriétés Un Zéro Infini
Sites	Nombres Voir liens vers les sites sur les nombres

Références

On trouve ces explications dans de nombreux livres

en particulier ceux qui relatent l'historique des nombres.

On peut tout de même citer un livre facilement abordable:

Le monde des nombres de Bastien Fernandez

N'oublions pas le bouquin de référence, très abordable:

Merveilleux nombres premiers - Jean-Paul Delahaye.

Ce livre permet de voyager au cœur de l'arithmétique et de toutes les notions relatives aux nombres.

Voir Bibliographie du débutant.