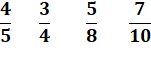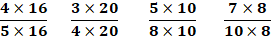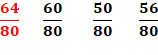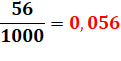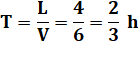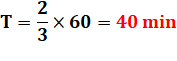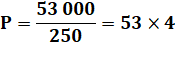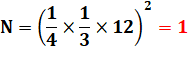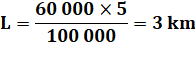|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
Citation de novembre 2023
|
En un quart de siècle, les élèves
français ont perdu l’équivalent d’un an en termes de niveau. Autrement dit,
un élève de 4ème, en 2018, a le niveau d’un élève de 5ème en 1995. Les résultats de français et de
mathématiques, matières fondamentales, sont les plus alarmants. Pour preuve,
à l’entrée en 6ème, 1 élève sur 3 ne sait pas lire correctement, et seule la
moitié d’entre eux trouve la bonne réponse à la question "Combien y a-t-il de quarts d’heures dans ¾ d’heure
? Gabriel Attal (Ministre de l'Éducation)- novembre 2023 |
Voir Pensées et Humour
|
|
||||||||||||||||||||||||||
|
Problème 1 Joan a 12
pommes. Elle en mange quelques unes et il lui en reste 9. Quelles
est l'opération qui décrit ce qui s'est passé? |
|
|||||||||||||||||||||||||
|
Solution 1 Elle a 12
pommes, moins celles qu'elle mange, égal 9 pommes. Ce qui se traduit par
l'opération C. |
|
|||||||||||||||||||||||||
Voir
Soustraction – Initiation
|
Problème 2 Kim range
des œufs dans des boites. Chacune peut contenir 6 œufs. Il a 94 œufs à
ranger. Combien
lui faut-il de boites? |
Solution 2
Il
faut 16 boites |
Voir
Division – Initiation
|
Problème 3 Tom mange
Quelle
part du gâteau ont-ils mangé ensemble? |
Solution 3
|
|
Problème 3 bis Quelle
est la plus grande de ces quatre fractions?
Alternative Avec
réduction au même dénominateur
on aurait:
|
Solution 3 bis Il est plus facile de prendre la valeur décimale que de calculer avec le même
dénominateur. Les
factions deviennent: 0,8 0,75 0,625 0,7 C'est la
première qui est la plus grande. |
Voir
Fractions – Initiation
|
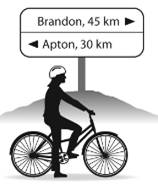
Problème 5 Mary
quitte Apron et roule durant 2 heures à la même vitesse. Elle atteint le
panneau. Mary continue à rouler à la même vitesse vers Brandon. Combien
de temps mettra-t-elle pour aller de ce panneau à Brandon? 1½ h
ou 2 h ou
3 h ou 3½ h |
|
||||||||
|
Solution 5 Le
premier trajet dure 2 heures pour 30 km Le second
est 1,5 fois plus long et durera 2 x 1,5 = 3 heures Aussi: La
vitesse de Mary est de: 30 / 2 = 15 km / h Pour
faire 45 km il lui faudra: 45 / 15 = 3 heures. |
|
Voir
Vitesse
– Initiation / Problème
de débit
|
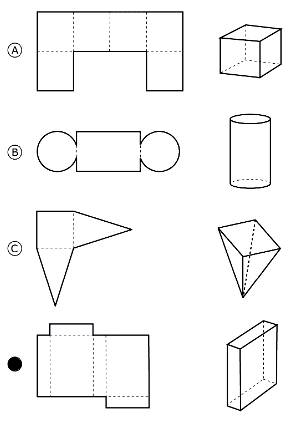
Problème 6 Ina a
trouvé ces patrons pour fabriquer des volumes. Quel
patron permet la réalisation du volume indiqué à son côté? Solution 6 A)
possède bien la quantité de faces, mais la forme en U ne convient pas: il y
aurait deux "fonds" et pas de "couvercle". B) la
forme est bonne, mais le rectangle n'est pas assez large pour s'appliquer à
la circonférence du disque. C) il
maque manifestement deux faces triangulaires. D) c'est
bien le patron du parallélépipède (proche de celui du cube). Cette fois, il y
a bien une oreille de chaque côté pour le "fond" et le
"couvercle". |
|
Voir
Patrons
du cube – Les 11 possibilités
|
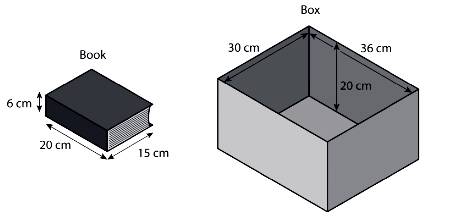
Problème 7 Ryan doit
ranger des libres dans un boite. Tous les livres ont la même taille. Combien
de livres peut-il ranger dans la boite? Solution 7 La
hauteur du livre (20 cm) correspond justement à la hauteur de la boite. Les
livres seront donc placés debout dans la boite. Avec 6 cm
par livre sur 36 cm de longueur de boite, il va 36 / 6 = 6 livres. Et ils
occupent la moitié de la boite. En effet,
sur la largeur de la boite, il va deux livres l'un derrière l'autre (2 x 15
cm de livres pour 30 cm de boite). Il est
possible de ranger 2 x 6 = 12 livres dans la boite. |
Tailles du livre et de la boite
Solution en tableau
|
Voir
Volume
du pavé (parallélépipède)
|
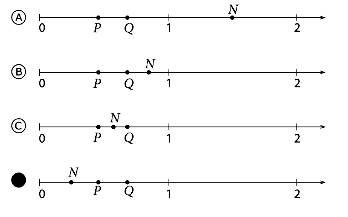
Problème 8 P et Q
sont des fractions sur la droite des nombres telles que sur la figure du
haut. N = P x Q Montrez
la position de N sur la droite des nombres. Solution 8 Le
produit d'un nombre par un nombre plus petit que 1 est un nombre encore plus
petit. Ex: 5 x 0,2 = 1 plus petit que 5. C'est
vrai même si le deuxième nombre est lui-aussi plus petit que 1. En fait le produit
sera plus petit que le plus petit des deux nombres. Ex: 0,5 x 0,2 = 0,1 plus
petit que 0,2. La
réponse est bien la proposition D. |
Énoncé
Propositions
|
Voir Multiplication – Initiation / Proportions
|
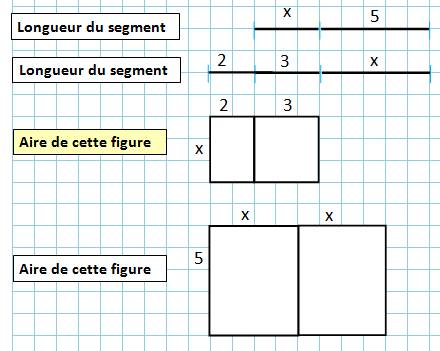
Problème 9 Quelle
est la figure qui représente: 2x + 3x Solution 9 Il s'agit
d'une somme de produits. Or, un produit ne représente pas une longueur mais
une aire. L'aire d'un rectangle. L'aire
des deux rectangles sur la figure du bas est égale à 5x + 5x. Ce n'est pas la
bonne réponse. Par
contre, l'aire des deux rectangles au-dessus, est bien égale à 2x + 3x. |
Propositions
|
Voir Aires
– Formules
|
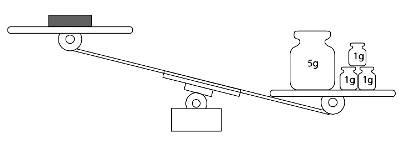
Problème 10 Jo a
trois blocs de métal. Le poids de chacun est le même. Deux pesées:
l'une avec un bloc et 8 grammes; et, l'autre avec 3 blocs et 20 grammes. Quel
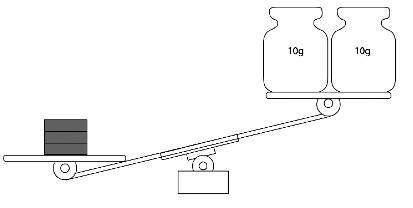
serait le poids d'un bloc métallique: 5, 6, 7 ou 8 grammes? Solution 10 Première
pesée: B < 8 Deuxième
pesée 3B > 20 Une inégalité peut être divisée par un nombre positif. Divisions par 3 B > 6,66 Parmi les
propositions, seule 7 grammes convient
(supérieure à 6,6 et inférieure à 8). |
Pesée avec 1 bloc
Pesée avec 3 blocs
|
Voir Énigmes de
pesées / Égalités
|
Problème 11 Le
tableau exprime une relation entre x et y. Complétez
le tableau avec 2, 3, 4, 5 ou 6. Solution 11 On pense
d'abord à une proportion y = kx. Pas possible, k serait variable d'une ligne
à l'autre. Alors une
relation en y = ax + b. Pensons à
la plus simple. Par exemple 7 = 4a + b avec a = 1 et b = 3. Mais, avec 13 = 7
+ 6, ça ne marche pas. La piste
est bonne, essayons b = a – 1. Bingo: le
nombre manquant est 3. |
Relation entre x et y
Solution en tableau
|
Voir Suites de nombres
|
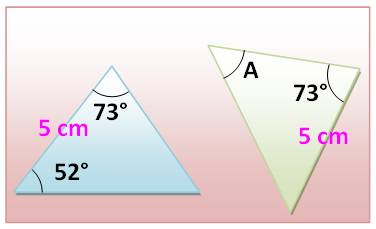
Problème 12 Ces deux
triangles sont égaux*. Quelle
est la valeur de l'angle A ? 52, 55, 65, 73 ou 75°. Solution 12 Notons
que le côté de 5 cm est côtoyé par l'angle à 73° et aussi par l'angle 52°
lequel n'est pas indiqué sur la figure de droite. L'angle A
n'est pas celui à 52°. Mais la
somme des angles d'un triangle vaut 180°: A + 52 +
73 = 180 A = 180 –
52 – 73 = 55° *isométriques, ou congruents
(anglais) |
|
Voir Triangles
égaux / Somme
des angles du triangle
Tous ces
exemples sont extraits de Example
Mathematics Items – TIMSS 2015
Autres
exemples en anglais en TIMSS Mathematics
Items
![]()
|
|
|||
|
Question |
Réponse |
Commentaires |
|
|
Division et puissance de 10 56 / 1000 = ? Voir Division
/ Puissance
de 10 |
|
56 / 10 = 5, 6 56 / 100 = 0,56 56 / 1000 = 0,056 |
|
|
Vitesse Je pars à 6 heures de chez moi et je marche à 6
km/h. Combien de temps vais-je mettre pour arriver à
l'école qui se trouve à 4 km ? Voir Vitesse |
|
En 1 heure, je fais 6 km En 60 min, je fais 6 km En 10 min, je fais 1km En 40 min, je fais 4 km |
|
|
Restes de la division Malik prépare des cookies. Quand il essaie de les partager équitablement
entre 2, 3 ou 4 de ses amis, il en reste toujours 1 pour lui. Combien de cookies a-t-il pu préparer ? 9, 11 ou 13 ? Voir Division
euclidienne / |
13 = 3 x 4 + 1 13 = 4 x 3 + 1 13 = 6 x 2 + 1 BON |
11 = 2 x 4 + 3 => non 9 = 3 x 3 + 0 = > non |
|
|
Comparaison Marc a préparé 53 kg de confiture répartie dans
des pots de 250 g. Il possède trois placards de 7 étagères chacun où
il peut ranger 10 pots par étagère. A-t-il assez de place pour ranger ses pots de
confiture ? |
Pas assez! |
250 g = 1/4 de kg 4 fois plus de pots que de kg => 53 x 4 = 212 pots 3 placards x 7 étagères x 10 pots = 210 rangements de pots. |
|
|
Périmètre Julia court autour d'un terrain rectangulaire de
20 mètres de long et 5 mètres de large. Elle fait 10 tours et demi du terrain. Combien d'hectomètres a-t-elle parcouru ? Voir Périmètre |
L = 10,5 x 2 (20+5) =
525 m = 5,25 hm |
Périmètre du terrain: 2 fois (20 + 5) m = 50 m 10 fois le tour: 500 m Sans oublier le demi tour => 5 x 100 + 25 m = 525 m = 5,25 hectomètres |
|
|
Unités Sophie a couru 10 hectomètres et 3 décamètres. Quelle distance a-t-elle parcouru en mètres ? Voir Préfixe
des unités |
L = 1000 + 30 = 1030m |
10 hm = 10 x 100 m
= 1000 m 3 dam = 3 x 10 m
= 30 m |
|
|
Calcul Quel est le carré du quart du tiers de 12 ? Voir Fractions |
|
Tiers de 12 = 4 Quart de 4 = 1 Carré = 1² = 1 |
|
|
Pourcentages Luc achète 450 kg de grains de café. Il torréfie ce
café qui perd 20 % de son poids. Quelle quantité de café torréfié peut-il vendre ? Voir Pourcentages |
Q = 450 x 0,8 =
360 kg |
Perte de 20% Reste 80% pour la vente |
|
|
Longueur Pour construire l'arc de Triomphe miniature,
Mahaut a utilisé 60 000 allumettes. Sachant qu’une allumette mesure en moyenne 5 cm,
quelle longueur, en kilomètres, obtiendrait-on si on plaçait les 60 000
allumettes bout à bout ? |
|
60 000 x 5 = 300 000 cm = 3000 m = 3 km |
|
|
Nombre à deviner Je suis un nombre entier composé de cinq
chiffres, sachant que tous les chiffres sont différents. Je suis un nombre pair. Les chiffres
sont écrits en suivant l’ordre décroissant. Le chiffre des dizaines est le double de celui
des unités. Le chiffre des unités de mille est le triple de
celui des unités. Le chiffre des dizaines de mille est la somme de
celui des centaines et des dizaines. Qui suis-je ? Voir Pourcentages
/ Nombres à
deviner |
N= DM cdu (dix milliers, milliers, centaines, dizaines et unités) u = {0, 2, 4, 6 ou 8} d = 2u M = 3u => M = 6, u = 2 et d=
4 =>
N = D6 c42 Différents et
décroissants => c = 5 => N =
D6 542 D = c + d => D = 9 => N = 96 542 |
|
|
Énigme avec additions Michel possède 2 873 pin's. Sa sœur Leïla en
possède 561 de plus que lui. Michel donne 193 pin's de sa collection à sa
sœur. Avec ceux que leur père vient de lui donner,
Leïla en a maintenant 4 177. Combien de pin's Leïla a-t-elle reçus de la part
de son père ? Voir Initiation
au calcul – Index |
Michel: 2 873 |
Leila: 2 873 + 561 = 3 434 |
|
2 873 – 193 = 2 680 |
3 434 + 193 = 3 627 |
|
|
|
4 177 – 3 627 = 550 |
|
Tous ces exemples sont extraits de la page de
franceinfo:
QUIZ.
Addition, multiplication... Avez-vous encore le niveau d'un élève de CM2 en
maths ?
– Élise Lambert – 12/02/2018
![]()
|
Tests d'évaluation d'entrée en sixième (2022) |
|
|
Selon BFMTV.com
sur la base de l'évaluation nationale de septembre 2022
|
|
|
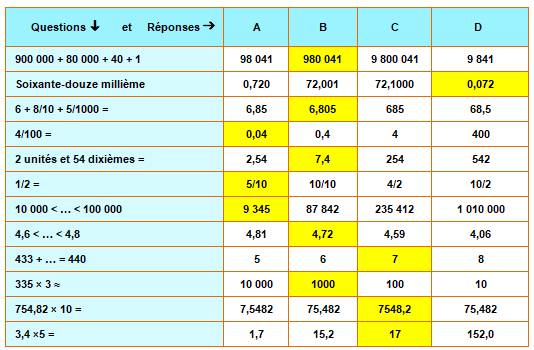
Solutions
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()