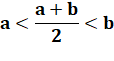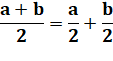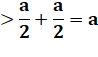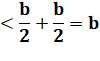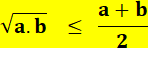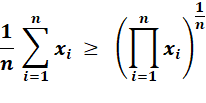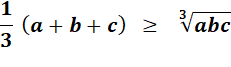NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/06/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	COMPTER
Débutants Général	MOYENNES				Glossaire Général
INDEX Moyenne	Débutants	Introduction	Comparaison	Confiance
		Somme entiers	Carré magique
		Sommaire de cette page >>> Comparaison avec les nombres >>> Démonstration muette >>> Comparaison entre elles >>> Moyenne géométrique et arithmétique >>> Tendances >>> Illustration géométrique

MOYENNES

Comparaison de la plus petite à la plus grande.

Comparaison avec deux nombres
Soit a et b tels que	0 < a < b
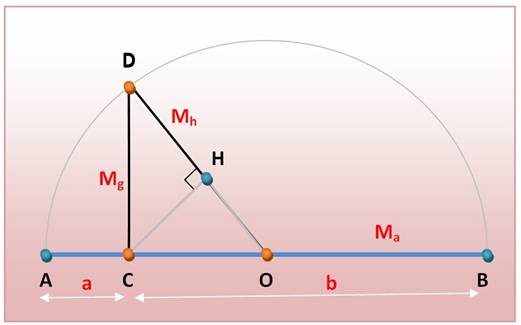
Moyenne arithmétique	La moyenne arithmétique est située entre les deux nombres.
Démonstration	0 < a < b
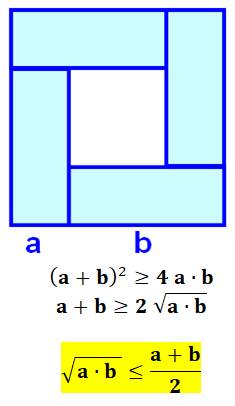
Moyenne géométrique
Démonstration	De même pour la moyenne géométrique.
	0 < a < b

Démonstrations muettes		haut

Voir Brève 500-995

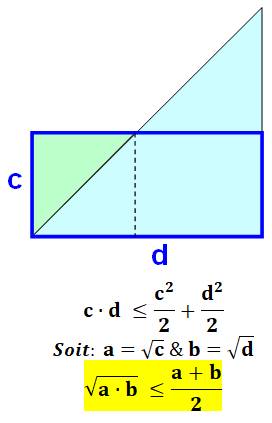
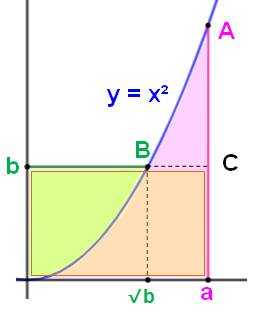
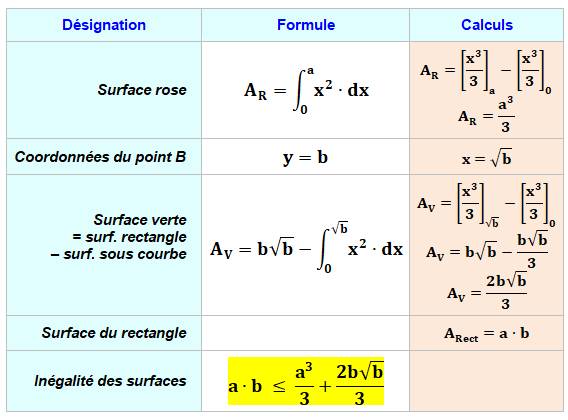
Autre inégalité par comparaison des surfaces sous la courbe y = x²

Voir Calcul par intégration (primitives)

Comparaison
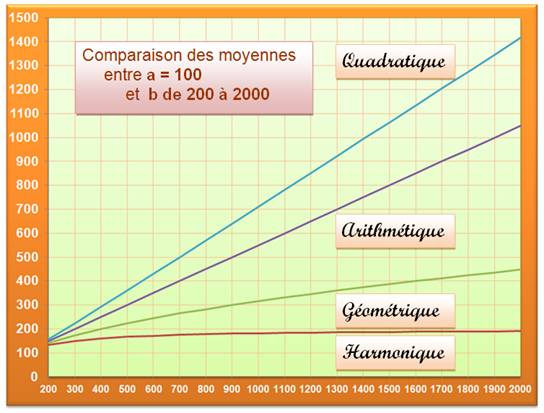
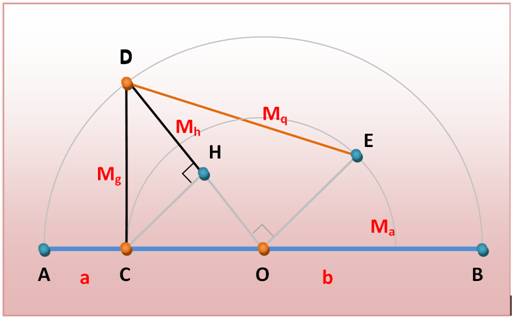
Si a < b (positifs) alors, on trouve dans l'ordre du plus petit au plus grand: a Moyenne harmonique Moyenne géométrique Moyenne arithmétique Moyenne quadratique b Outil souvent utilisé en démonstration: La moyenne géométrique est inférieure ou égale à la moyenne arithmétique.

Moyenne géométrique < Moyenne arithmétique
Quel est le plus grand: x² + y² ou 2xy, avec x différent de y? Quelle conclusion tirer ? D'une manière générale: Exemple pour trois valeurs au cube:

Voir Résolution de l'énigme 711

Tendances
Courbes montrant l'évolution de chacune des moyennes. l Cas de deux données dont l'une est maintenue fixe (a = 100) et l'autre (b) varie de 200 à 2000.

Comparaisons géométriques
Cette représentation est attribuée à Archimède

Suite	Moyenne quadratique Moyenne – Index
Voir	Dénombrement Moyenne et médiane Opérations
Cette page	http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm