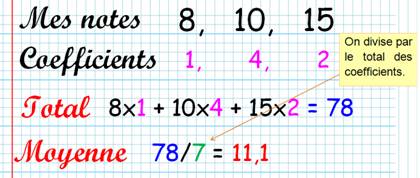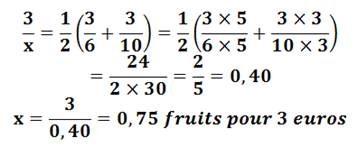|
||||||||||||||||||||||||||||||||||||||||
![]()
|
MOYENNES Débutants
La moyenne classique, comme la moyenne des notes
en classe, semble évidente à calculer: Additionnez toutes les notes et
divisez par la quantité de notes. Pourtant, il existe plusieurs types de moyennes.
Elles peuvent réserver des surprises. |
|
Moyenne – Une sorte de lissage |
|
|
La
moyenne est une valeur unique qui vise à représenter la tendance d'une
collection de valeurs. Elle
remplacerait toutes ces valeurs pour donner un même résultat global si tout
s'était toujours passé de manière égale. Elle
représente une sorte d'équilibre, de nivellement, de lissage entre toutes les
valeurs de la collection. Dans le langage courant, la moyenne
est, en fait, la moyenne arithmétique,
mais il en existe d'autres selon les besoins. |
|
|
|
||
|
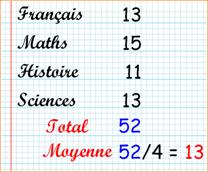
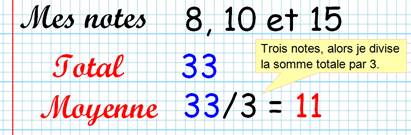
C'est la moyenne des notes, méthode
bien connue à l'école. Tout se passe comme si cet élève avait eu un 11 dans chacune des trois
matières. La moyenne (arithmétique) donne une valeur qui résorbe les excès et
les manques. L'élève s'efforce d'avoir une bonne note pour faire remonter la
moyenne! Lorsqu'il n'y a pas beaucoup de valeurs, il est possible d'évaluer de
tête les écarts et de donner immédiatement la valeur de la moyenne. |
Méthode
directe
Méthode
des écarts
|
|
"On ne demande qu'à en rire"
|
Émission de Laurent Ruquier
où les humoristes sont notés par un jury de quatre personnes, puis vient
s'ajouter la note du public. La note est sur 20, et
le seuil critique pour l'élimination est 12. Plutôt que de faire le calcul
sur les notes, il est plus facile de calculer les écarts par rapport à 10 ou
à 12.
|
|
Moyenne arithmétique
pondérée – Comme au lycée |
|
|
|
C'est la moyenne des notes au lycée lorsque certaines matières
comptent plus que d'autres. Tout se passe comme si, on avait obtenu autant de notes que l'indique
le coefficient. |
|
|
Suite Moyenne arithmétique
|
|
||
|
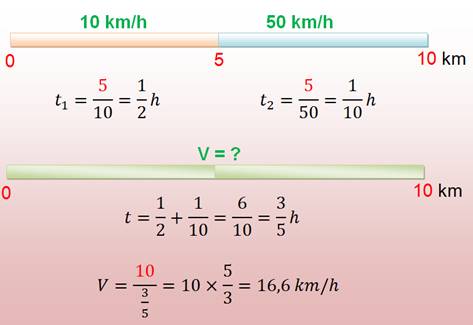
C'est la moyenne utilisés pour calculer des vitesses moyennes. Rappelez-vous, les calculs de vitesses fourmillent de pièges; celui de
la moyenne des vitesses, aussi! Dans l'exemple la vitesse moyenne n'est pas
30 km/h. Avec les problèmes de vitesses, le truc est de toujours s'en remettre
à la formule L
= V . t Cette moyenne fait intervenir, non pas la somme comme pour la moyenne
arithmétique, mais la somme des inverses des nombres. |
Aller: 5 km à 10 km/h puis 5km à 50 km/h Retour: à quelle vitesse constante tout en mettant le même temps?
Réponse 16,6 km/h. |
|
Suite
Moyenne
harmonique
|
|
||
|
C'est la moyenne qui permet de calculer les intérêts que rapporte une
somme placée à la banque. En effet, l'intérêt s'applique chaque année au capital plus les intérêts qui ont déjà été produits. Cette moyenne fait intervenir la multiplication et les racines. Pour deux valeurs, la moyenne géométrique est la racine carrée du produit des deux
valeurs. Et dans le cas général, la moyenne est la racine nième du produit des n
valeurs. |
En plaçant à 2% sur 1 an et 10% l'année suivante, c'est comme si on
plaçait la même somme à 5,9% par an sur les deux ans. |
|
Suite Moyenne géométrique
En pratique: ordre de grandeur
|
On
dispose de deux estimations en puissances de 10 (souvent une borne inférieure
et une borne supérieure quelle est la meilleure estimation moyenne ? C'est la
moyenne géométrique (pas la moyenne arithmétique). Exemple:
ma valeur se situe entre 3 102 et 4 104. Plus
les coefficients sont proches et plus la valeur approximée se rapproche de la
valeur moyenne. Cas
pas très sympa: si la demi-somme des exposant est impaire ! |
Merci à Romain RAMEL pour cette idée
|
|
||
|
Problème Un marchand vend:
La fin du marché approche et
il lui reste 50 pommes et 50 poires.
Il décide de les vendre 3 euros les 8. La
moyenne entre 6 et 10 est 8, pense-t-il. Empoche-t-il un bénéfice ou
fait-il une perte? Ce qui se produit Le commerçant croit faire la
bonne moyenne. Or, avec des divisions (3 euros divisés par 6 …), il faut se
méfier! La moyenne à utiliser n'est pas la moyenne arithmétique, mais la
moyenne harmonique. Calcul à effectuer sur la base d'une paire de
fruits
|
Solution La vente globale des 2 x 50
derniers fruits lui rapporte: 3 x 100/ 8 = 37,5
euros. En les vendant normalement,
il aurait gagné: 3 x 50 / 6 + 3 x 50 / 10 = 25 + 15 = 40 euros. Discussion Manifestement, la moyenne
entre 3 euros les 6 et un 3 euros les 10 n'est pas 3 euros les 8. Le bon raisonnement en termes de moyenne Une poire coûte: 300 / 6 =
50 cts. Une pomme coûte: 300 / 10 =
30 cts. En proposant une pomme et
une poire, il doit vendre la paire de fruits: 50 + 30 = 80 cts. Coût moyen d'un fruit: 80 /
2 = 40 cts. Revenus pour les 100 fruits:
40 euros. Ce qui revient à 7,5 fruits
pour 3 euros en moyenne. |
|
Voir Fractions
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()