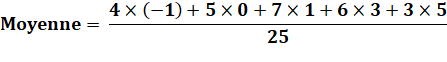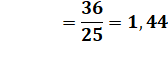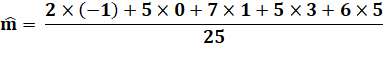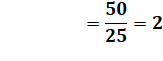|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Série statistique incomplète Résolution pas à pas
Je choisis parmi trois niveaux d'explications: 1.
Nous
allons supposer le problème résolu et ajuster progressivement les paramètres.
>>> 2.
Ayant
compris le mécanisme, nous présenterons une approche directe du problème. >>> 3.
Solution
en bref. >>> |
Ce problème
est issu d'un forum sur Internet, lui-même extrait d'un manuel scolaire.
|
|
||
|
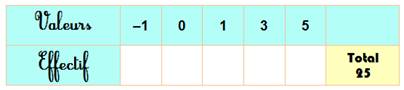
Le total
de l'effectif est précisé dans le tableau:
25. Il peut
s'agir d'élèves dans une classe, ou de morceaux de viande chez un boucher, ou
… |
Effectif =
25 La statistique
porte sur un échantillon de 25 éléments,
sans que l'énoncé précise de quoi il s'agit. Peu importe! |
|
|
Énumérons
les 25 éléments (élèves, morceaux de viande …) un par un:
|
||
|
|
||
|
La valeur caractérise
chacun des éléments de la statistique: taille, poids, sexe, qualité, etc. des
élèves, des moreaux de viande, … Les
valeurs données dans l'énoncé sont des nombres relatifs. On ne dit pas à
quoi ils correspondent. Peu importe! |
Exemple classique d'un caractère statistique: la
taille des hommes. La valeur du caractère
pour un élément (un individu) est alors, par exemple: 1,73 m. Exemple de correspondance des valeurs: Qualité des morceaux de viande dans le stock du boucher:
|
|
Vocabulaire
|
En
langage courant, on comprend mieux individu
plutôt qu'élément. C'est pourtant le
second mot qui est choisi car plus général. En
langage courant, on comprend mieux qualité
plutôt que caractère. C'est pourtant le
second mot qui est choisi car plus général. Pour un homme dont la taille a une valeur de 1,75 m; |
Voir Vocabulaire des
statistiques
|
|
||
|
Nous
avons nos 25 morceaux de viande (exemple). Il s'agit de les caractériser par
une valeur indiquant la qualité (le caractère) de chacun. Reprenons
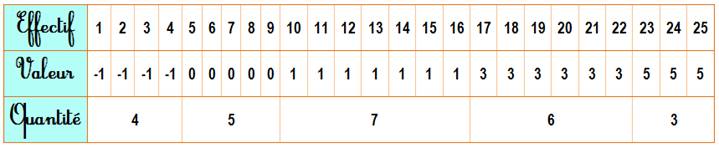
le tableau de l'effectif détaillé et remplissons le au hasard.
En ayant
conservé l'ordre de la qualité (de -1 à 5), il est plus facile de compter la
quantité par catégorie. Par exemple: 4 morceaux de viande sont en -1, donc
mauvais et sans doute à jeter. Sauf chance
exceptionnelle, ce tableau ne répond pas, bien sûr, aux critères de l'énoncé. Note: la première
ligne devrait être nommée échantillon de la population et non effectif. |
||
|
Moyenne: c'est la somme pondérée ramenée à un seul individu. C'est
aussi la somme des 25 valeurs divisée par 25. |
Notez bien que la moyenne
exigée par l'énoncé est 2 et non 1,44. Il faudrait ajouter plus de morceaux
de bonne qualité pour faire remonter la moyenne. En fait, la valeur de la
somme pondérée doit être égale à 50 et non 36. |
|
|
|
||
|
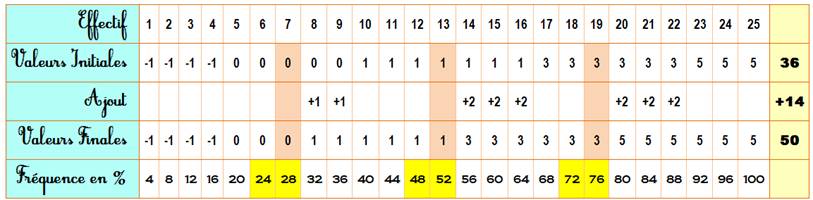
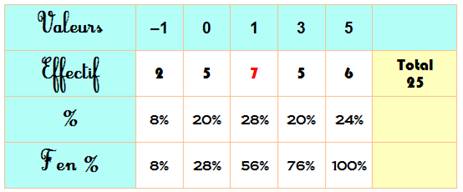
En
reprenant notre exemple, calculons les pourcentages de valeurs en dessous
d'un effectif donné; ce pourcentage est appelé fréquence.
Avec ce
tableau, on déduit, par exemple que 64% des morceaux de viande sont de
qualité 1 ou inférieure. |
||
|
Médiane = 1 (Élément
13) |
Pour le morceau 13, on trouve autant de morceaux
moins bons que meilleurs (12 de chaque côté). C'est le moment ou la fréquence passe à 50%. Avec le treizième morceau, on est sûr qu'il y a
autant de morceaux de chaque côté et, pour 13, la valeur est 1. Note: oui, mais
quelques uns des morceaux de chaque côté du 13 sont aussi à 1. C'est vrai!
Mais, c'est la définition de la médiane. Valable pour des caractères qui
prennent plus de valeurs que dans cet exemple. |
|
|
Quartiles Q1 = 0 Q3 = 3 (Éléments
7 et 19) |
Ce sont les valeurs (marron) situées après les
transitions indiquant plus de 25% et
de 75% (jaunes). Note: Q1 est la
valeur de l'élément 7 qui a bien 6 éléments à gauche et 18 à droite. Q2 est la
valeur de l'élément 19 qui a bien 18 éléments à gauche et 9 à droite. Notez bien que les valeurs
exigées par l'énoncé sont satisfaites pour la médiane et les quartiles. Reste
à ajuster la moyenne en répartissant
autrement les valeurs sans changer médiane et quartiles. |
|
|
|
|
|
Reprenons
le tableau. La médiane et les quartiles sont en marron et ne doivent par être
modifiée (0, 1 puis 3). Par contre les valeurs intermédiaires peuvent être
augmentées pour atteindre 50. Il manque 16.
Sur la
ligne valeurs finales, on a bien: moyenne
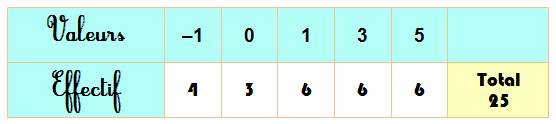
= 50 / 25 = 2; médiane = 1 et quartiles = 0 et 3. Solution n°1 Présentation
sous la forme demandée en comptant les populations de même valeur. Il y a 4
fois la valeur -1; 3 fois la valeur 0; etc.
|
|
|
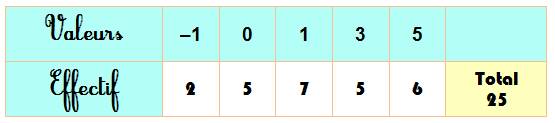
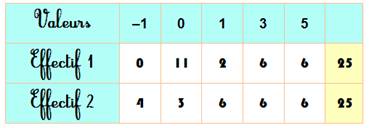
Solution n°2 Nous
aurions pu ajuster le tableau initial en diminuant le nombre de morceaux
mauvais (en -1). Ce qui donne cette nouvelle solution: Et le
bilan:
|
|
|
Nous avons trouvé deux solutions; il en existe d'autres. Ce cheminement pas à pas nous a permis d'apprivoiser le vocabulaire
spécifique aux statistiques: valeurs et effectif de la population (ou de l'échantillon).
La moyenne se calcule directement
en effectuant la moyenne pondérée. Pour la médiane et les quartiles, il est nécessaire de
"déplier" l'effectif pour mettre en évidence la fréquence de ces
valeurs. |
![]()
|
|
||
|
Maintenant
que nous avons compris le vocabulaire et la "mécanique", voyons
comment obtenir la solution plus directement. Reprenons
l'une des solutions. |
|
|
|
Calcul de la moyenne |
|
|
|
Calcul de la médiane |
La médiane est la valeur pour l'élément n°13 (12 de part et d'autre). Le tableau montre (2+5
= 7) valeurs à gauche du 7 et (5+6=11) valeurs
à droite. Le treizième élément est quelque part dans le
compte des 7 du centre. Or, pour cet effectif,
la valeur est 1. La médiane est égale à 1. |
|
|
Calcul de Q1 |
Le premier quartile indique que 25% de l'effectif
est inférieur à cette valeur. En prenant l'effectif pour la valeur -1, nous avons
5%; pas assez. En prenant l'effectif pour les valeurs (-1 et 0),
nous atteignons 28%; c'est plus que 25%. Q1 = 0. |
|
|
Calcul de Q3 |
Le troisième quartile indique que 75% de
l'effectif est inférieur à cette valeur. En prenant l'effectif pour les valeurs (-1 à 1),
nous avons 56%; pas assez. En prenant l'effectif pour les valeurs (-1 à 3),
nous atteignons 76%; c'est plus que 75%. Q3 = 3. |
|
|
Approche directe Avec cette méthode, la première étape consiste à remplir le
tableau proposé au hasard. Puis, à calculer les paramètres statistiques et
les ajuster en procédant par rectification progressive du tableau initial. Un
tableur peut s'avérer de bon secours. Approche détaillée (déploiement des effectifs) Pour plus d'assurance, l'approche détaillée est conseillée. La consigne est donc:
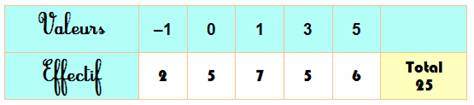
Il s'agit de remplir le tableau avec des (-1, 0, 1,
3, 5), dans cet ordre, sachant que la somme des valeurs est 50. Il existe de nombreuses solutions dont les deux
extrêmes ci-dessous:
Tableau de réponse
|
Annexe
|
|
||
|
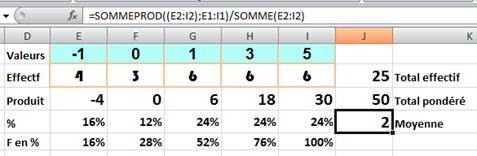
La fonction moyenne pondérée sur Excel se calcule
avec SOMMEPROD. Voyez la formule dans la fenêtre en haut. Le résultat de
calcul est encadré. Les autres calculs sont classiques. |
|
|
Voir Tableur
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |