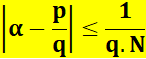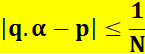|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Théorème de Dirichlet Comment approcher un nombre
irrationnel avec une fraction optimum ? ou, quels sont les multiples d'un nombre
irrationnel se rapprochant le plus d'un nombre entier? Approche et démonstration à la façon
de Dirichlet lui-même; en utilisant
le principe des tiroirs. Le théorème en bref Pour
tout nombre irrationnel, il existe une infinité de fractions qui s'approchent
du nombre de plus en plus près. L'erreur est inférieure au carré de la
fraction "1 / dénominateur". La fraction 22/7 est proche de Pi à
moins de 1/9². Pi –
22/7 = 0,0012… et 1/49 = 0,02… |
Vous pouvez voir un exemple d'application avant d'entrer dans la théorie
laquelle théorie est tout à fait
abordable comme vous allez le voir.
|
|
||
|
|
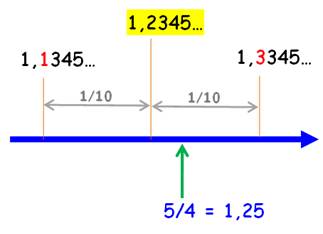
Prenons le nombre 1,23456 … Cherchons une fraction qui approche ce nombre à
1/10 près. Nous trouverons assez rapidement que 5/4 = 1,25
fera l'affaire. L'illustration le montre bien:
|
|
|
On peut dire que 1,2345…
est proche de 5/4 à 1/40
près; ou en multipliant par 4, que: 1,2345… x
4 = 4,938…
est proche de 5 à 1/10 près On répond alors à la question: quel est le
multiple du nombre irrationnel qui se rapproche le plus d'un nombre entier? |
||
|
|
||
|
|
|
|
|
Théorème Si Les deux traits
verticaux indiquent qu'il faut prendre la valeur absolue (ignorer le signe). Ou, en multipliant la relation précédente par q:
Autrement
dit: tel que Voir note ci-dessus |
||
|
|
||
|
[ 0,
1/N[ [1/N, 2/N[ [2/N, 3/N[ … [N-1/N, 1[
{ 0 } {
{ 2 { 3 … { N
On les note:
{ r . |
[0,
1[ veut dire que le 0
fait partie de l'intervalle, alors que le 1 n'en fait par partie. Le principe
des tiroirs se met en action:
Il y a N + 1 objets dans N tiroirs, un des tiroirs contiendra au moins 2 objets. Alors,
une tranche contiendra forcément deux parties décimales. |
|
|
Monde des parties décimales des
multiples d'alpha, et leur place dans des tranches de largeur 1/N.
Une des tranches 1/N
contient forcément deux parties décimales. {xx} veut dire partie décimale du nombre. |
|
Théorie
Autrement dit:
|
Se faire une idée Dans l'exemple ci-dessus,
avec N = 10, les valeurs de r et s seraient: r = 9 => 9 x 1,234… = 11,110… s = 5 => 5 x 1,234… = 6,172… La différence
4 x 1,234… = 4,938 … Qui s'approche à moins de 1/10 du nombre entier q
= 5 qui n'est autre que la différence des parties entières: 11 – 6 = 5.
Valeur bien inférieure à 0,1 = 1/10 |
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Livre |
|
|
Cette page |
![]()