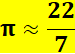NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/08/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Théorie des Nombres
Débutants Fractions	Théorème de Dirichlet				Glossaire Fractions
INDEX Th des Nbs	Introduction	Théorème	Application à Pi	Tableur
		Duffin-Schaeffer
		Sommaire de cette page >>> Calcul d'une réduite de Pi >>> Justification >>> Dirichlet >>> Réduite de Pi au 1/1000

Théorème de Dirichlet

Application au calcul des réduites de Pi

Méthode de calcul, et explications avec Dirichlet.

Voir Table des réduites de Pi

Calcul d'une réduite de Pi
Quelle est la fraction optimale qui approche Pi avec un dénominateur inférieur ou égal à 10? Voici une recette qui permet de calculer cette valeur, applicable dans le cas général de n'importe quel nombre irrationnel.	Nous le savons depuis longtemps, il s'agit de la fraction 22/7. La méthode est basée sur le théorème de Dirichlet.
Première étape Prendre la partie décimale des multiples de Pi. Pour un dénominateur de 10, il faut les 11 multiples de k = 0 à k = 10. Observons les dixièmes et notons les cas d'égalité de ces dixièmes: égalité pour k = 1 et k = 8, égalité pour k = 2 et k = 9, et égalité pour k = 3 et k = 10.	Pi = 3,141592654 k k x Partie décimale de Pi 0 0 1 0,141592654 2 0,283185307 3 0,424777961 4 0,566370614 5 0,707963268 6 0,849555922 7 0,991148575 8 0,132741229 9 0,274333882 10 0,415926536
Seconde étape Intéressons-nous au premier cas. Le dénominateur de la fraction recherchée est égal à la différence entre les valeurs de k: N = 8 – 1 = 7 Prenons maintenant la partie entière des deux multiples de Pi. pour k = 1, le multiple de Pi vaut 3,14 … pour k = 8, le multiple de Pi vaut 25,132 … La différence des parties entières nous donne le numérateur de la fraction recherchée: 25 – 3 = 22	Voici les deux cas retenus (k = 1 et k = 8) avec la partie décimale des multiples et la valeur des multiples: 1 0,141592654 3,141 … 8 0,132741229 25,132… Voici le calcul de la fraction (dite réduite) approximant Pi: N = 25 – 3 = 22 D = 8 – 1 = 7

Les deux autres cas Avec k = 2 et k = 9, on trouve évidemment la même valeur. Avec k = 3 et k = 10, itou!

2 0,283185307 6,28… 9 0,274333882 28, 27… N = 28 – 6= 22 D = 9 – 2 = 7 3 0,424777961 9,42 … 10 0,415926536 31,41 … N = 31 – 9 = 22 D = 10 – 3 = 7

Élément de justification Avec k = 1, la partie décimale est comprise entre 0 et le premier dixième. C'est le cas aussi pour le huitième multiple de Pi; sa partie décimale est située dans le premier dixième. Alors écrivons leur appartenance à cette première tranche de 1/10 au moyen d'une inégalité. Avec la soustraction des inégalités; la plus grande moins la plus petite. Attention, les inégalités sont subtiles: il faut inverser l'égalité soustraite! On se souvient que la différence des parties entières vaut 22. Passons en valeur absolue. Si l'on divise tout par 7. Ce qui veut dire que Pi est égal à 22/7 à moins de 1/70 près. En fait, nous faisons nettement mieux comme le montre les valeurs numérique.

La partie décimale est en fait égale au nombre auquel on retire sa partie entière: 0,1415… = 3,1415… - 3 Que l'on peut écrire: 0,1415… = – [] Écrivons cette relation pour k = 8: 0,1327 … = 8x – 8x[] 0,0012… < 0,014… et 0,0012 = 1 /790 bien mieux que 1/70.

Et Dirichlet ?
Le théorème de Dirichlet est bien utile pour la raison suivante: il confirme qu'il y a toujours une solution à cette méthode. En effet: Lorsque nous calculons les multiples et que nous classons leurs parties décimales, il existera toujours deux valeurs placées dans la même tranche de dixième. Ou, toute autre tranche que nous choisirions pour obtenir plus de précision.	Théorème général Si est un nombre irrationnel et M un nombre entier positif, alors il existe un rationnel p/q dont le dénominateur q est compris entre 1 et M et tel que Théorème appliqué Avec et M = 10, alors il existe un rationnel p/q = 22/7 dont le dénominateur 7 est compris entre 1 et 10 et tel que

Réduite de Pi suivante
Si nous cherchons dans les centièmes nous retrouverons 22/7 tant la première réduite est "puissante". Il nous faut aller fouiller dans les millièmes. Avec un tableur, on calcule les 1001 multiples de Pi, et on trie tous nombres selon leur millième. Lorsque deux millièmes sont égaux, bingo! On calcule la fraction. Avec k = 121 et k = 8, nous trouvons la première égalité des millièmes, d'où la fraction: Vous feriez le même calcul avec l'occurrence suivante: k = 114 et k = 1.	Millième des multiples de Pi k k. Pi millièmes ordonnés 0 0,000 0,000 106 333,009 0,009 99 311,018 0,018 92 289,027 0,027 85 267,035 0,035 78 245,044 0,044 71 223,053 0,053 64 201,062 0,062 57 179,071 0,071 50 157,080 0,080 43 135,088 0,088 36 113,097 0,097 29 91,106 0,106 22 69,115 0,115 15 47,124 0,124 121 380,133 0,133 8 25,133 0,133 114 358,142 0,142 1 3,142 0,142 107 336,150 0,150 100 314,159 0,159 93 292,168 0,168 L'écart donné par l'inéquation est 1/113000 = 8,8 10^-6, alors que la réduite 355/113 s'écarte de Pi de 0,26 10^-6

---

Suite	Théorème de Dirichlet Valeurs de Pi Lejeune-Dirichlet Table des réduites de Pi
Voir	Dénombrement et tiroirs Inventaire des outils mathématiques
Aussi	Compter - Index Compter Jeux Factorielle et ses cousins Jeux de hasard Grenouilles Probabilités
Livre	Tangente HS 39 – L'art du dénombrement – Avril 2010
Cette page	http://villemin.gerard.free.fr/aMaths/ThNb/ThDirEx.htm