|
Édition du: 27/01/2025 |
|
INDEX |
Topologie |
||
![]()
|
Problème du rectangle inscrit Problème du carré inscrit –
Conjecture de Toeplitz Une conjecture
simple à énoncer: on peut inscrire un carré ou un rectangle sur toute courbe
fermée continue et lisse. Le cas du carré
est toujours une conjecture ouverte. Le cas du rectangle
a été résolu en 2020. La
démonstration est originale. Elle procède en plusieurs étapes dont une qui
fait appel à la topologie.
|
||
|
|
Sommaire de cette page >>> Problème du rectangle inscrit >>> Cas des courbes simples >>> Principe de la démonstration pour le
rectangle >>> Bilan et extrait de la démo complète >>> Historique |
Débutants Glossaire |
Anglais: The inscribed
square problem / The rectangular peg problem / Toeplitz’s square peg conjecture
|
|
||
|
Résolution en 2020 Le
problème du rectangle inscrit est un vieux
problème qui vient d'être résolu pendant le confinement du printemps 2020 par
Joshua Greene et Andrew Lobb. Une
première avancée avait été faite vers
la fin des années 1970 par Herbert Vaughan. |
Origine C'est Ott Toeplitz, un mathématicien allemand qui
formule cette conjecture en 1911. Sa conjecture s'appliquait au carré, cas toujours
non résolu. Malgré sa formulation simple, de nombreux mathématiciens
s'y sont cassé les dents. Comment appliquer les propriétés du carré sur les
points d'une courbe quelconque ? |
|
|
Théorème Toute courbe fermée contient au moins un
quadruplet de points qui forme un rectangle. Pour toute courbe lisse de Jordan (courbe simple)
et tout rectangle R dans le plan euclidien, il existe un rectangle similaire
à R dont les sommets sont sur la courbe.
|
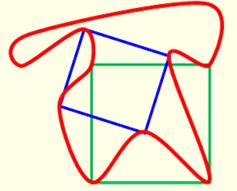
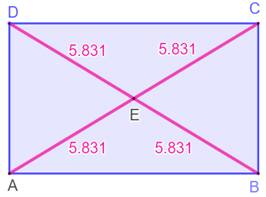
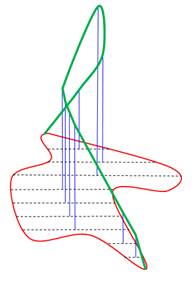
Exemple
Sur la courbe rouge, on a été capable d'y
inscrire au moins un carré. Est-ce toujours faisable ? |
|
Voir Brève 59-1178
|
|
||
|
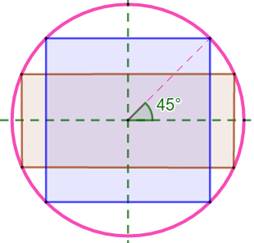
Cercle Le carré
est inscriptible dans le cercle
et de multiples façons par rotation. Le
rectangle l'est également de multiples façons par rotation est aussi par
changement de taille. Avec deux
points sur la circonférence, il est toujours possible de construire un
rectangle inscrit. |
|
|
|
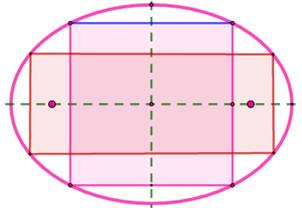
Ellipse Le carré
est inscriptible dans l'ellipse
d'une seule façon et son côté est fonction des
mesures des axes de l'ellipse. Le
rectangle inscrit a des côtés
parallèles aux axes. Il y en a une infinité. Note: impossible d'inscrire un rectangle en oblique. |
|
|
|
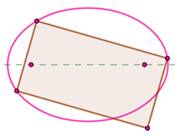
Conclusion Pour
ses deux courbes symétriques fermées, la conjecture est vérifiée. |
||
|
|
||
|
Description intuitive de la
démonstration La
démonstration procède en plusieurs étapes et plusieurs mondes mathématiques. Voici une
explication imagée. La traduction mathématique n'est accessible qu'à des experts
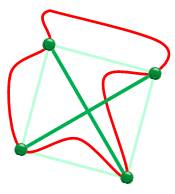
du domaine (Voir le texte des auteurs). Étape 1: diagonales Plutôt qu'au rectangle, on va s'intéresser aux
deux diagonales: elles ont mêmes mesures et elles se coupent en leur milieu. Le principe consiste alors à faire courir deux
segments sur la courbe et à détecter les cas d'égalité avec intersection au
milieu. |
Diagonales égales
Critères satisfaits et Non respectés
|
|
|
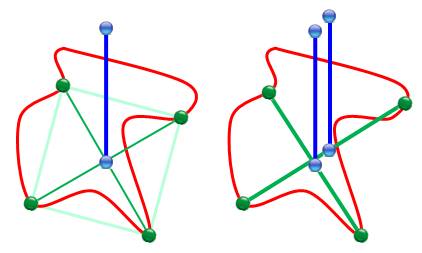
Étape 2: hauteurs Astuce !
Dresser une perpendiculaire au milieu de chacun des segments et lui donner la
longueur du segment (bleu). On
obtient une figure dans l'espace (en 3D). Il suffit
désormais de balayer la courbe et de détecter des hauteurs identiques (à
gauche) et de rejeter tous les autres cas (à droite). |
Traits bleus confondus = présence
d'un rectangle
|
|
|
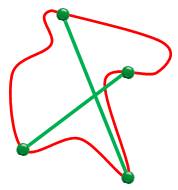
Étape 3: surface En
balayant tous les couples de points, on crée un ensemble de points, lieu des
sommets des hauteurs. La courbe
verte est un échantillon. Avec tous les points, la courbe se transforme en
une surface qui enveloppe complètement la courbe. Cette surface est continue.
Une petite variation sur les points entraine un petit déplacement sur la
surface. Les
points où les hauteurs sont égales sont des points singuliers de la surface; des
points atteints par deux routes différentes; la surface se coupe elle-même. Comment
détecter ces singularités ? |
Lieu de l'extrémité de la hauteur
|
|
Vidéo
|
Même sans connaitre l'anglais, je vous propose de visionner la vidéo
du site: New
Geometric Perspective Cracks Old Problem About Rectangles – Kevin
Harnett. Vous y retrouverez les figures de cette page avec des animations. Les images 3D de cette page sont extraites de cette vidéo. |
![]()
|
Étape 4: projection C'est ici
qu'intervient les techniques de la topologie. On coupe
la courbe et on la "pose" sur l'axe des x pour y faire courir un
des points de la paire (bleu). On fait courir l'autre sur l'axe des y (bleu).
Une paire de points devient une paire de nombres (de coordonnées) et donc, un
point désigné dans le plan. Attention,
on a artificiellement coupé la courbe; il faut penser à la reconnecter en
"enroulant" les axes (traits rouges). Oui, on obtient un tore ! |
La courbe transformée
Chaque point du plan comme chaque point de la
surface du tore représente une paire de points sur la courbe initiale. |
|
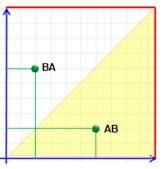
Étape 5: correction Nous
sommes allés un peu vite ! Une paire
AB représente deux segments AB et BA. Il ne faut en retenir qu'un seul. Sur le
plan, ces deux segments sont représentés par deux points symétriques par
rapport à la diagonale. Conséquence:
il ne faut garder qu'une moitié du plan (partie jaune). Une opération
de recomposition des bords conduit à abandonner le tore et à passer à un ruban de
Möbius. |
Seule une moitié du plan doit être conservée,
alors chaque point de la surface du ruban représente une paire ordonnée de points de la courbe initiale. La bordure du ruban correspond aux paires de
points confondus sur la courbe initiale. |
|
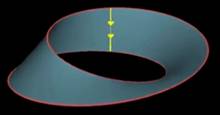
Étape 6: la solution ! Si on
rapproche la surface "des hauteurs" et le ruban de Möbius:
Il est impossible d'appliquer le bord du
ruban sur la courbe (rouge sur rouge) sans forcer le ruban à se croiser. Et
le croisement est la singularité que nous cherchons. Donc: il
existe un endroit où la surface se recoupe et ce fait entraine que deux
diagonales égales se coupent en leur milieu et par conséquent un rectangle
existe quelque part. Note: la
démonstration complète fait intervenir une surface à quatre
dimensions: la quatrième étant l'angle
d'orientation des diagonales >>> |
Chaque point sur la surface comme chaque point du
ruban correspond à une paire de points sur la courbe initiale. Imposer la superposition topologique des deux figures
entraine un croisement obligatoire, lequel est le témoin de la présence d'un
rectangle. |
![]()
|
Une démonstration très sophistiquée
mathématiquement mais qui dans son principe expose une méthode originale et
émouvante pour un amateur de mathématiques. |
Une idée du niveau mathématique nécessaire pour aborder la
démonstration complète

Extrait de: The Rectangular Peg Problem –
Joshua Evan Greene, Andrew Lobb – Cornell University – 19 May 2020
L'historique
suivant est établit d'après ce même site
|
1911 – Toeplitz – Formule la conjecture du carré
inscrit. 1913 – Emch – Résoud la conjecture pour des
courbes lisses convexes. 1929 – Schnirelman – Traite le cas des courbes
lisses de Jordan mais avec une hypothèse qui ne couvre pas tous les cas. 1981 – Vaughan – Avancée sérieuse dans le cas des
rectangles. Il introduit l'idée de s'intéresser au lieu des
hauteurs représentant les diagonales. Ce lieu contient obligatoirement un
point de triple intersection (auto-intersection) témoin de la présence d'un
rectangle. Le ruban de Möbius est déjà utilisé. 1991 – Griffiths – Croit détenir une preuve pour
le cas du rectangle; infirmée en 2008 par Matschke. 2018 – Hugelmeyer – Réussit à résoudre quelques
cas complémentaires selon l'angle des diagonales (angle d'aspect) en
recourant à la quatrième dimension. Lui aussi, fait intervenir le ruban de
Möbius pour conclure. 2020 – Joshua
Evan Greene et Andrew Lobb – Démonstration
du théorème du rectangle inscrit en prolongeant les travaux de Vaughan et en
s'appuyant sur la nouvelle idée de Huglemeyer pour analyser le ruban de
Möbius: comment implanter (typologiquement) le ruban de Möbius (2D) dans un
objet à quatre dimensions ? Il faut, en quelque sorte, donner à chaque point
du ruban, une adresse à quatre nombres:
Green et Lobb avaient déjà démontré qu’il était
possible d’intégrer la bande de Möbius dans un espace (symplectique) à quatre
dimensions d’une manière qui respecte les règles de l’espace. Ce qu'ils
voulaient vraiment savoir, c'était si chaque rotation de la bande de Möbius
croise la copie originale. En fait, deux bandes de Möbius qui se croisent
sont équivalentes à une bouteille de Klein, qui se croise dans ce type
d'espace. Et si vous faites pivoter une bande Möbius de sorte que la copie
pivotée ne coupe pas la copie originale, vous avez essentiellement produit
une bouteille de Klein qui ne se coupe pas. Mais une telle bouteille de Klein est impossible
dans un espace symplectique à quatre dimensions. Par conséquent, chaque
rotation possible de la bande de Möbius intégrée doit également se croiser,
ce qui signifie que chaque courbe fermée et lisse doit contenir des ensembles
de quatre points qui peuvent être réunis pour former des rectangles de tous
les rapports d'aspect. |
![]()
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()