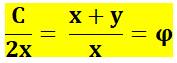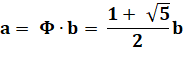NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/02/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 20		Page 30		Page 40		Page 50			Page 60
	Page 50 (980-999)		Page 51 (1000-1019)		Page 52 (1020-1039)		Page 53 (1040-1059)		Page 54 (1060-1079)
	Page 55 (1080-1099)		Page 56 (1100-1119)		Page 57 (1120-1139)		Page 58 (1140-1159)		Page 59 (1160-1179)

BRÈVES de MATHS – Page 59

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

1160. Faire cinq triangles avec trois
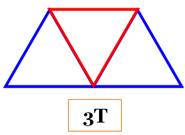
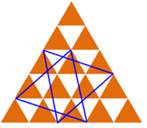
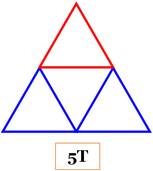
Énigme Trois triangles adjacents comme sur cette figure. Comment déplacer un seul de ces triangles pour obtenir cinq triangles ? Solution Une solution simple et élégante consiste à retourner le triangle rouge pour créer deux nouveaux triangles: le triangle central de même aire que les trois autres; et le grand triangle englobant les quatre triangles. Cependant, il existe quelques autres solutions.		Figure initiale Solution
Brèves associées	>>> Triangle en carrés – Calcul de l'aire		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Cinq triangles avec trois triangles		>>> Triangles – Curiosités

1161. Simplification sous radicaux
Brèves associées	>>> Calcul avec racines carrées		>>> Brèves Algèbre – Index
Pour en savoir plus	>>> Calculs avec radicaux >>> Racines – Index		>>> Nombre 0,41442… >>> Nombre 0,26794…

1162. Nombre d'or dans le carré
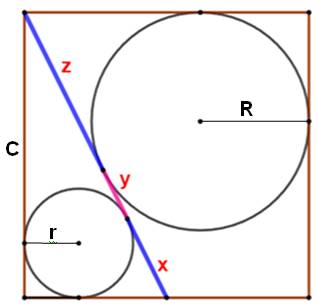
Construction Un carré et une semi diagonale joignant un sommet au milieu du côté opposé. Les deux cercles inscrits dans les espaces créés. Les points de tangence partage la semi-diagonale en trois segments de longueur x, t et z Propriété On a aussi: y = r = R/2 x + y = C/2		Figure
Brèves associées	>>> Nombre d'or et Th. de Ptolémée		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Nombre d'or dans le carré – Démo		>>> Carré et deux cercles

1163. Intersection droite-cercle
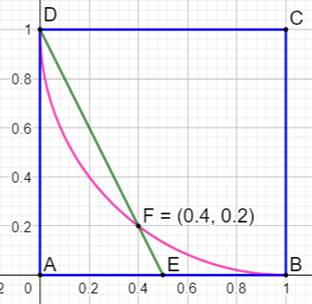
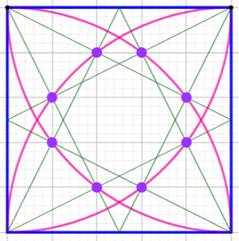
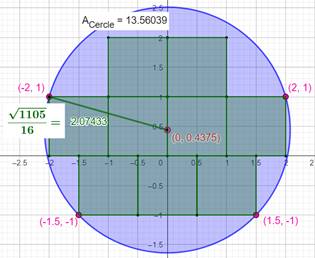
Construction Un carré dans lequel on trace un quart de cercle et une semi-diagonale issue d'un sommet et joignant le milieu du côté opposé. Quelles sont les coordonnées du point d'intersection? Pistes Avec l'équation de la droite et celle du cercle, on calcule le point d'intersection. Calculs Les coordonnées des points sur les cercles sont des nombres rationnels.		Figure Les huit points d'intersection
Brèves associées	>>> Parenthèses: (a+b)(c+d)		>>> Brèves Algèbre – Index
Pour en savoir plus	>>> Équation de la droite		>>> Équation du cercle

1164. Triangle de Kobon
Combien ? Avec sept droites, combien de triangles arriverez-vous à construire. Quelle est la quantité maximale ? Réponse La figure montre onze triangles. Avec une droite de plus, il est possible d'en faire apparaitre quinze. A vos crayons … Solution
Brèves associées	>>> Triangle de Kepler (nombre d'or)		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangles de Kobon		>>> Quantité de triangles

1165. Premier et base de numération
Question Est-ce qu'un nombre premier en base décimale demeure premier dans d'autres bases? Réponse OUI !		Question Une suite de chiffres peut-elle représenter un nombre premier dans une base mais un nombre composé dans une autre base ? Réponse OUI !
Explications Le fait d'être premier ou composé est simplement une propriété du nombre lui-même quelle que soit la façon dont il est écrit. Imaginez avoir N cailloux et disposez les en formation rectangulaire. Si vous ne pouvez faire qu'une rangée, la quantité de cailloux est un nombre premier. Vous notez que cette propriété subsiste quel que soit le nom que vous lui donner. Par exemple n = 15 en décimal, F en hexadécimal ou même XV en chiffres romains. Mais c'est le même alignement de cailloux.		Explications Supposons qu'une chaîne de trois chiffres représente un nombre premier positif p dans une base donnée b, où b est un entier supérieur à 1. Évidemment, p doit être un nombre premier impair. Si nous changeons b en b+1, alors la chaîne de trois chiffres qui représentait un nombre premier impair représente maintenant un nombre pair positif supérieur à 2, qui doit donc être composé.
Brèves associées	>>> Diagramme de Ferrers		>>> Brèves Th. des Nombres – Index
Pour en savoir plus	>>> Premier et base de numération		>>> Nombres premiers – Propriétés

1166. Salade de chiffres
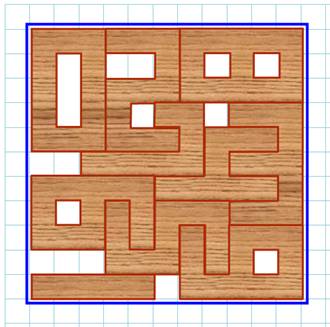
Chiffres en bois objet d'un puzzle Réunir ces chiffres inscrits dans une grille 3×5 dans un cadre carré de dimension: 11×11) Origine Commercialisé sous le nom: disponible chez les marchands de puzzles.		Solution
Brèves associées	>>> Séquence miroir		>>> Brèves Puzzle – Index
Pour en savoir plus	>>> Écriture des chiffres >>> Chiffres		>>> Jeux et énigmes – Index

1167. Construction des fractales
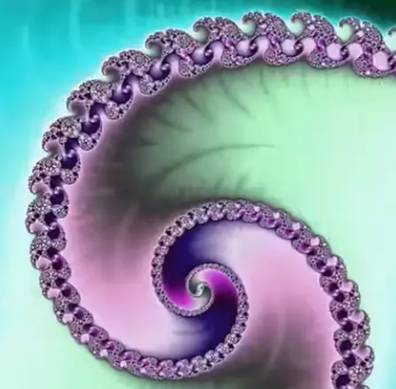
Principe de construction de l'image Imaginez un balayage du plan en lignes et colonnes. Tous les points sont méthodiquement passés en revue. Chacun de ces points est analysé pour décider quelle couleur lui associer. Principe de coloration des points Le traitement en chaque point est d'une rare simplicité (c'est ce qui rend les fractales si fascinantes ! ). Il s'agit d'une fonction de récurrence qui indique comment le résultat suivant est obtenu à partir du résultat précédent. Par exemple en prenant son carré plus une constante. Alors, de deux choses l'une: la fonction stagne ou la fonction croit et la couleur est choisie pour témoigner de la vitesse de croissance. Après analyse de tous les points, la forme fractale se dessine.		Résultat prodigieux à partir d'une formule simple
Brèves associées	>>> Fractale de Fibonacci		>>> Brèves Fractales – Index
Pour en savoir plus	>>> Programmation des fractales		>>> Fractales

1168. Magie des nombres de Kaprekar
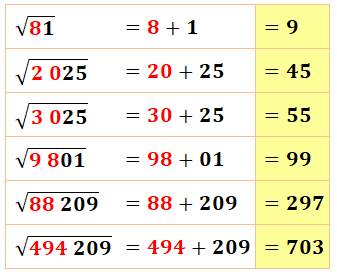
Racines carrés magiques Pour ces nombres, la racine se calcule facilement: Prendre la partie gauche du nombre, et Ajouter la partie droite. Attention Cela ne marche (hélas) que pour les nombres de Kaprekar. Les premiers nombres (racines) 1, 9, 45, 55, 99, 297, 703, 999, 2223, 2728, 4879, 4950, 5050, 5292, 7272, 7777, 9999, 17344, 22222, …
Brèves associées	>>> Nombres fourchettes		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres de Kaprekar		>>> Nombres narcissiques

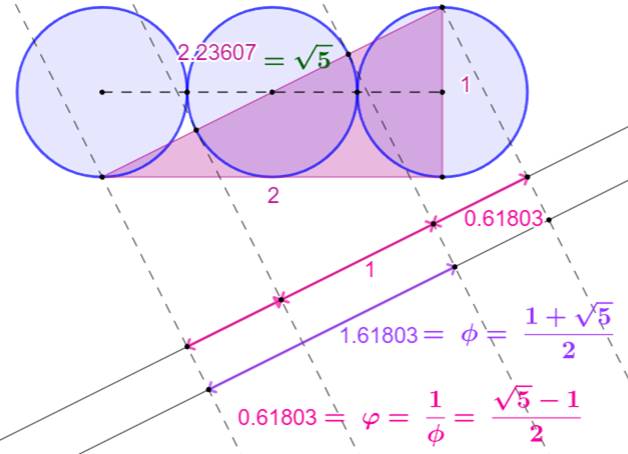
1169. Nombre d'or et trois cercles
Brèves associées	>>> Nombres d'or et d'argent	>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombre d'or et trois cercles	>>> Nombre d'or

1170. Jeu du 24
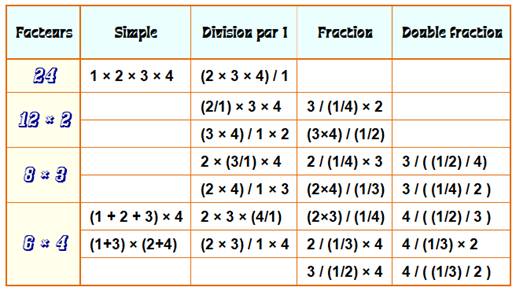
Règle du jeu Quatre nombres sont donnés. Avec les quatre opérations (addition, soustraction, multiplication, division) atteindre un résultat exactement égal à 24. Exemple Le tableau indique les solutions primitives pour les nombres: 1, 2, 3 et 4. Il existe d'autres solutions par permutations des nombres de ces solutions.
Brèves associées	>>> 200 avec neuf chiffres		>>> Brèves Jeux – Index
Pour en savoir plus	>>> Jeu du 24		>>> Jeux avec des nombres

1171. Les filles et les maths
Filles et garçons sont aussi capables en maths Pourquoi une sous représentation des filles dans certaines sciences (mathématiques, informatique, ingénierie…) et leur surreprésentation dans d’autres (biologie, chimie, médecine…) ? À 17 ans, une fille française sur deux n’étudie plus les mathématiques, contre seulement un garçon sur quatre. Celles-ci sont toujours considérées comme naturellement moins douées, alors que des décennies de recherche scientifique établissent que le sexe biologique ne détermine aucunement les capacités cognitives.		Le même cerveau et la même intelligence Un stéréotype du genre persiste et véhicule cette idée complètement fausse que les filles sont faites pour la littérature. Il y a encore 50 ans, on prétendait que le cerveau féminin n’était pas “câblé” de la même façon. Cette vision a depuis été démentie par les progrès des recherches en neurosciences L’intelligence n’est pas une affaire de sexe, et ce n’est pas elle qui fait la compétence en mathématiques : celle-ci ne s’acquiert que par l’entraînement.
Influence du vocabulaire On parle d’erreurs en mathématiques et de fautes de français, d’expression ou de goût ; et aussi d’erreurs de calcul et de fautes d’orthographe. Péchés véniels pour les uns (simples erreurs qui n’affectent pas vraiment la valeur de la personne), péchés presque mortels pour les autres. Cela en dit long, si l’on y réfléchit quelque peu, quant aux valorisations à l’œuvre dans le domaine du développement personnel et de la culture. Selon: Claude Lelièvre, Historien de l’éducation – Le Monde du 17/12/2024		Histoire pas si lointaine Lors de la création de l’enseignement secondaire public des jeunes filles en 1880, il s’agissait d’un enseignement de lettres et de langues vivantes modernes. En mathématiques, il est alors préconisé un programme essentiellement distinct de celui des jeunes gens. Le rapporteur s’en explique: Il serait inutile, et même fâcheux de développer chez les jeunes filles l’esprit d’abstraction ; d’autre part, elles n’ont que faire des mathématiques appliquées puisqu’elles ne deviendront pas ingénieurs.
Brèves associées	>>> Mnémotechnique des chiffres		>>> Brèves Enseignement – Index
Pour en savoir plus	>>> Bon en maths ? >>> Enseignement – Index		>>> Célèbres femmes scientifiques

1172. Aires et cercles
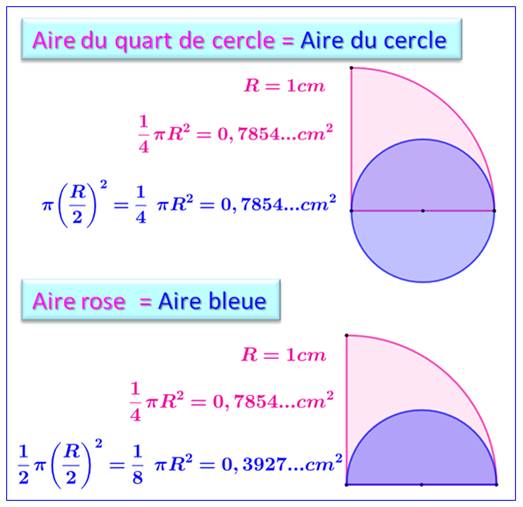
Note: en toute rigueur, on devrait dire: aire du disque et non cercle.
Brèves associées	>>> Aires dans le quart de cercle	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Cercle – Formulaire	>>> Cercle – Index

1173. Pavage d'Ammann-Beenker
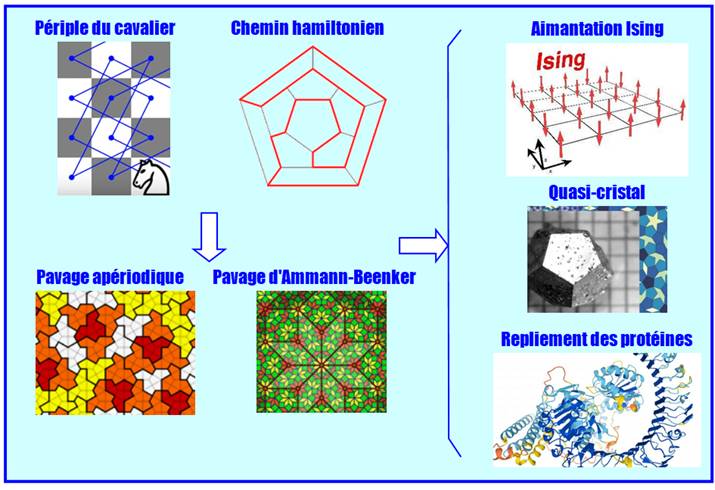
Comment révéler la structure interne de certains matériaux complexes comme les quasi-cristaux ? Une solution: la modélisation par un graphe dont on étudiera les propriétés. Notamment l'existence de chemins particuliers en boucle nommés chemins hamiltoniens. Problème résolu dans les cas simples en juillet 2024.
Brèves associées	>>> Graphe – Devinettes	>>> Brèves Graphes – Index
Pour en savoir plus	>>> Pavage d'Ammann-Beenker >>> Chemins hamiltoniens	>>> Périple du cavalier >>> Voyageur de commerce

1174. Carrés dans le cercle
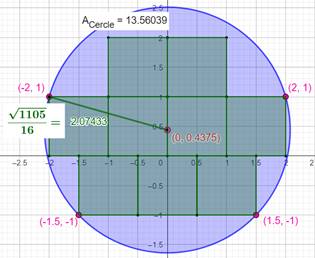
Rayon du cercle inscrivant n carrés unités Prenons n carrés unités et cherchons à les entourer par un cercle. Quelle est la meilleure disposition pour obtenir le plus petit cercle ? L'illustration montre le cas de neuf carrés unités. Le rayon minimum du cercle qui les contient vaut 2, 077… unités. Pour les cas de 1 à 10 au moins, le rapport entre l'aire du cercle et l'aire des n carrés tourne autour de 1,5. Ce qui veut dire que le taux de remplissage n'est pas très élevé. En gros, l'aire non couverte par les carrés (bleue) représente la moitié de l'aire des carrés (verte).
Brèves associées	>>> Carré dans le triangle rectangle		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Carrés dans le cercle		>>> Carrés dans le cercle – Énigme

1175. Quantité de rectangles
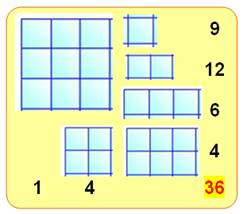
Théorème de Nicomaque La quantité de rectangles dans une grille de n×n carrés est égale à la somme des cubes de 1 à n ou encore au carré de la somme des nombres de 1 à n). Exemples Il y a 36 rectangles dans une grille 3×3 (Illustration). (1 + 2 + 3)² = 1^3 + 2^3 + 3^3 = 36 = 6² Il y a 2025 rectangles dans une grille 9×9. (1 + 2 + … + 9)² = 1^3 + 2^3 + … + 9^3 = 2025 = 45²		Dénombrement des rectangles dans la grille 3×3
Brèves associées	>>> Vingt propriétés du nombre 2025 >>> Combien de rectangles		>>> Brèves Dénombrement – Index
Pour en savoir plus	>>> Théorème de Nicomaque		>>> Quantité de carrés dans le carré

1176. Triangles dans le triangle
Dénombrement Dans ce triangle équilatéral de dimension 5, il existe 70 triangles. 25 triangles élémentaires de dimension 1; 23 triangles de dimension 2, 3, 4 et 5; et 22 triangles de dimension en racine de 3. Cas des triangles équilatéraux obliques (en √3) Leurs sommets sont sur les points de la grille mais leur côté n'épousent pas le lignage de cette grille.		Triangle de dimension 5 contenant 70 triangles équilatéraux de toutes tailles
Brèves associées	>>> Triangles dans le triangle		>>> Brèves Dénombrement – Index
Pour en savoir plus	>>> Triangles dans le triangle		>>> Triangle

1177. Pentagone – Construction
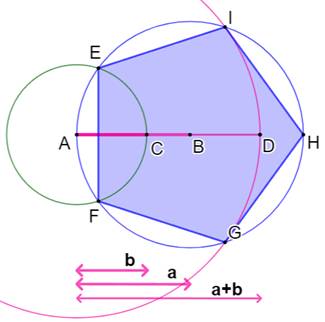
But Connaissant les longueurs a et b qui sont en divine proportion, construire un pentagone régulier. Divine proportion et nombre d'or (Phi) Construction Porter les trois longueurs a, b et a + b sur la même droite à partir du point A. Cercle de rayon b et de centre A (vert). Cercle de rayon a et de centre B (bleu). Intersections en E et F. Cercle de rayon a+b et de centre A (rose). Intersections en G et I. Le segment AB est prolongé pour donner le point H. Les points E, F, G, H et I sont les sommets du pentagone régulier.		Figure de construction du pentagone Propriété Les triangles du type EFI et FGI sont des triangles isocèles dorés.
Brèves associées	>>> Pentagone de l'arpenteur		>>> Brèves Constructions – Index
Pour en savoir plus	>>> Pentagone >>> Divine proportion et nombre d'or		>>> Construction – Index

1178. Problème du rectangle inscrit
Théorème Toute courbe fermée contient au moins un quadruplet de points qui forme un rectangle. Démontré pour le rectangle; pas pour le carré Origine C'est Ott Toeplitz, un mathématicien allemand qui formule cette conjecture en 1911. Résolution en 2020 Le problème du rectangle inscrit est un vieux problème qui a été résolu pendant le confinement du printemps 2020 par Joshua Greene et Andrew Lobb.		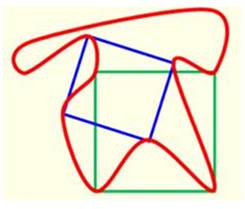Exemple Sur la courbe rouge, on a été capable d'y inscrire au moins un carré (ici, deux carrés). Est-ce toujours faisable ?
Brèves associées	>>> Rectangle dans le triangle rectangle		>>> Brèves Topologie – Index
Pour en savoir plus	>>> Problème du rectangle inscrit		>>> Topologie – Index

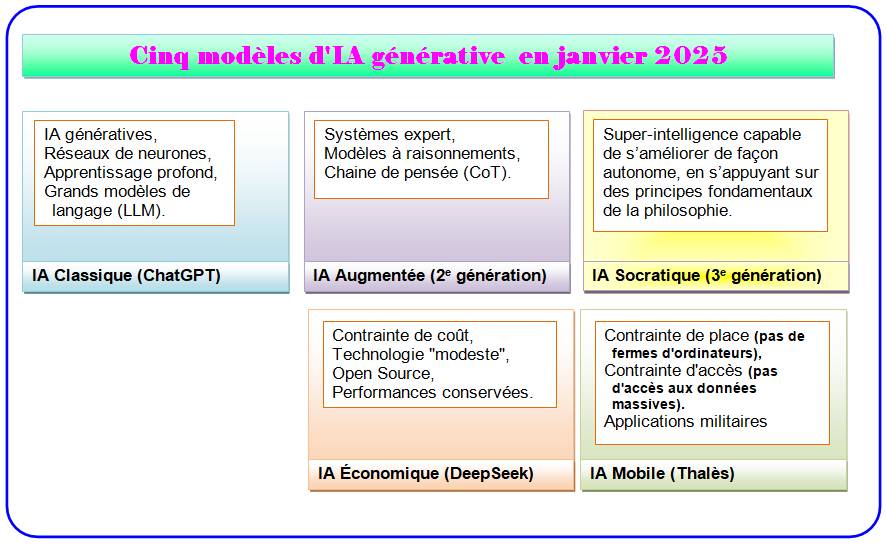
1179. IA Générative
Tentative de représentation à partir des annonces de la presse en début 2025
Brèves associées	>>> IA et indécidabilité	>>> Brèves Informatique – Index
Pour en savoir plus	>>> IA – Modèles en 2025	>>> IA – Introduction

Retour	Brèves de maths – Page 58
Suite	Brèves de maths – Page 60
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve59.htm

Quinze triangles de Kobon avec huit droites

Retour