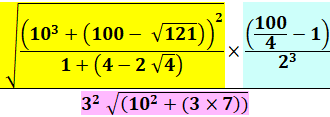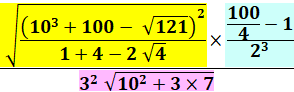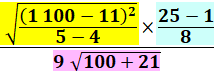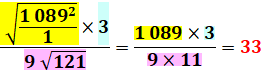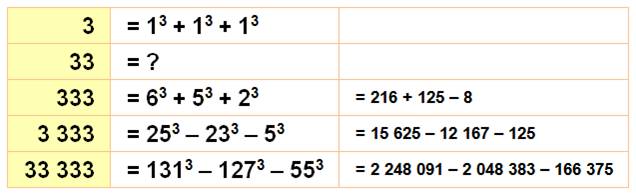|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombre
33 insolite Comment
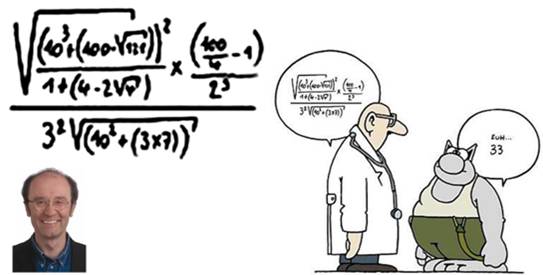
dire 33 en humour ou en trois cubes?
|
Développements
sur le nombre 33 (DicoNombre)
|
|
||
|
Dessin extrait de
La mathématique du chat (Texte mathématique de Justens,
illustré par Geluck) |
||
|
Formule explicitée et calculée |
|
|
|
Suppression des parenthèses inutiles |
|
|
|
Premiers calculs |
|
|
|
Suite et fin |
|
|
![]()
|
|
||
|
Problème
de la somme de trois cubes / Sums of three cubes problem or puzzle Nombre
égal à la somme de trois cubes / Integer equal the sum of three cubes Un problème facile à poser, mais très difficile à résoudre dans le cas
général. |
||
|
Disons le tout de suite pour
N < 101, on ne connait pas encore de solution pour N = 33, 42 et 74. |
Pour 33,
chacun des a, b, c > (1014)3 |
|
|
Pour les nombres N de 1 à 100
(Objet
de notre étude). |
Si N est
un cube, la somme comporte deux 0, comme 8 = 00 + 00 +
23 Certains
nombres sont somme de deux cubes, comme 7 = 13 + 23 |
|
|
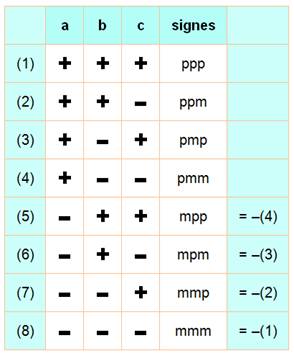
Les nombres a, b, c peuvent
être positifs ou négatifs. Sur les huit cas possibles seuls
quatre cas sont originaux; les quatre autres donnent la valeur négative de N. Les valeurs de a, b et c
sont croissantes (permutations possibles avec la même valeur de N):
|
|
|
|
On démontre que certains
nombres sont inaccessibles avec la somme de trois cubes, comme 4, 5, 13, 14,
… |
du fait que
Explications >>> |
|
|
On conjecture qu'il y a au
moins une solution pour tous les autres cas. |
Vers 2011, suite aux travaux d'Huisman (Lyon),
seules 23 cas restent non résolus: 33, 42, 114, 165, 390, 579, 627, 633, 732, 795, 906, 921, et 975 pour
une exploration des nombre jusqu'à 1015. |
|
|
On connait des solutions
paramétriques conduisant à une infinité de solutions pour certains nombres.
C'est le cas pour N = 1 ou N = 2. |
Ex: m = 1 103 + 93 – 123 = 1000 + 729 – 1728 =
1 73 – 53
– 63 = 2 |
|
|
Solutions: elles sont assez simples pour une grande majorité des nombres jusqu'à
100. Programmation simple et quelques minutes de calcul. Un peu plus long pour
quelques cas récalcitrant … |
La
recherche des solutions a passionné quelques personnes (voir références in fine). Le calcul devient vite long et l'enjeu consiste à
optimiser la programmation. |
|
|
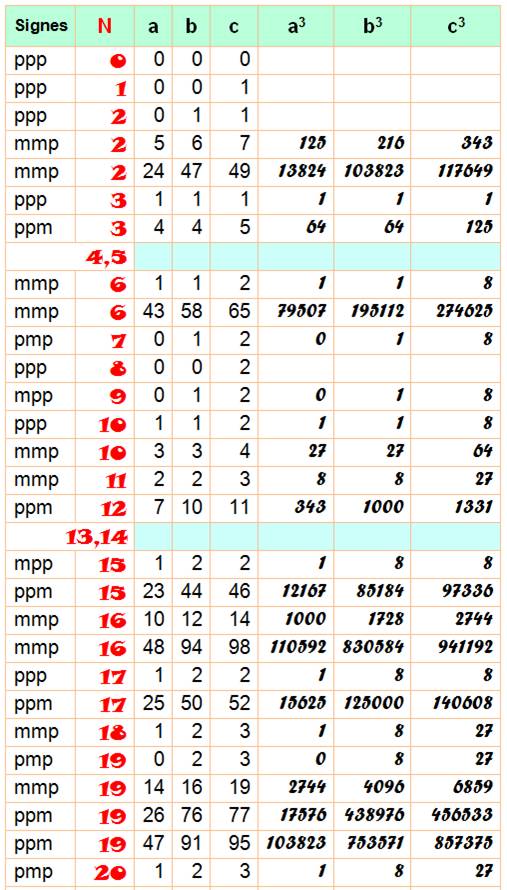
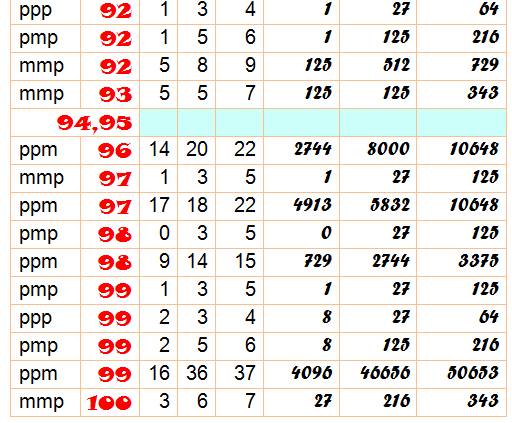
Tableau Certains nombres sont présentés avec plusieurs solutions. Toutes les présentations pour a, b et c jusqu'à 10 sont présentes. |
Signes: ppm indique que a et b sont positifs et c est négatif N de 0 à 100; en bleu, les nombres inaccessibles; en jaune les nombres
dont on ne connait pas de solution; en blanc avec le renvoi en fin de page >>> pour les solutions avec grands nombres. |
Voir Cubes et multiples de 9 / Somme de cubes
Tableau des solutions pour n de 0 à 100
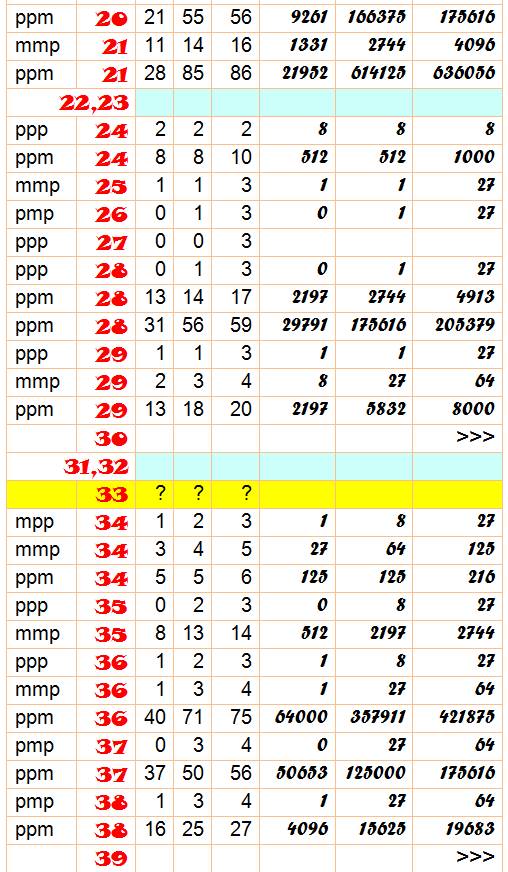
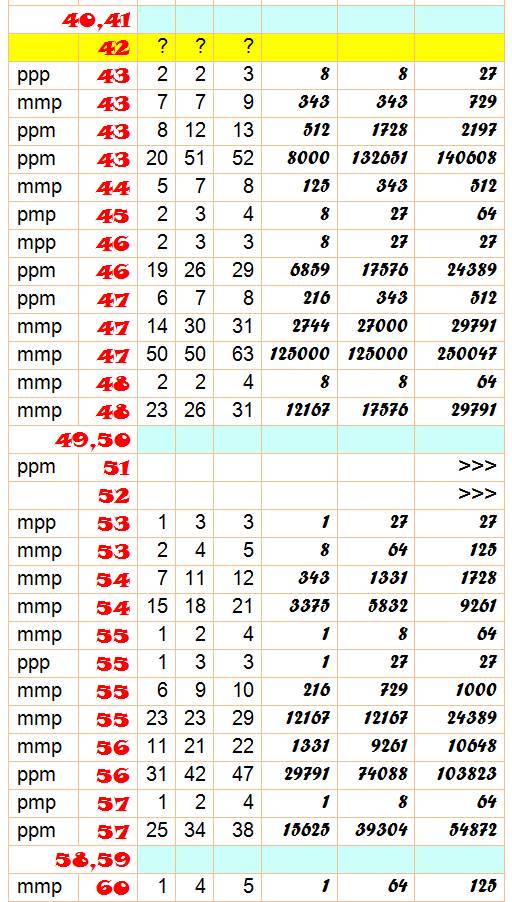
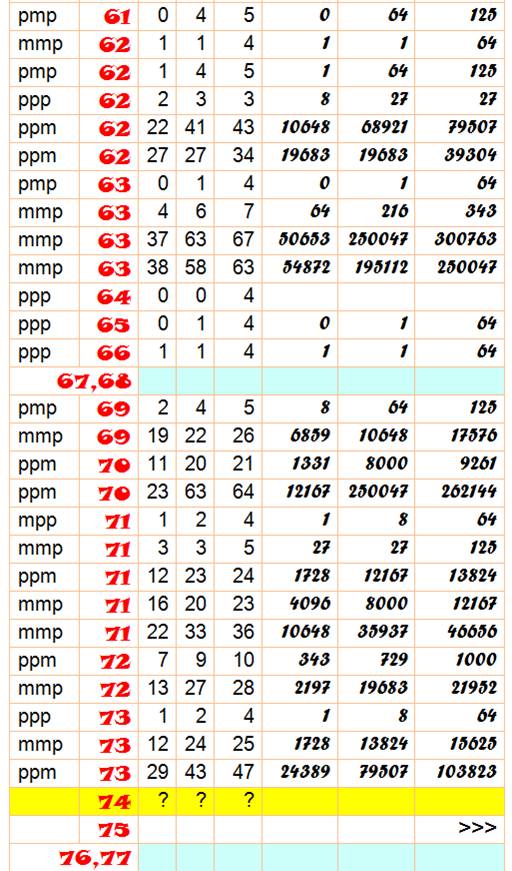
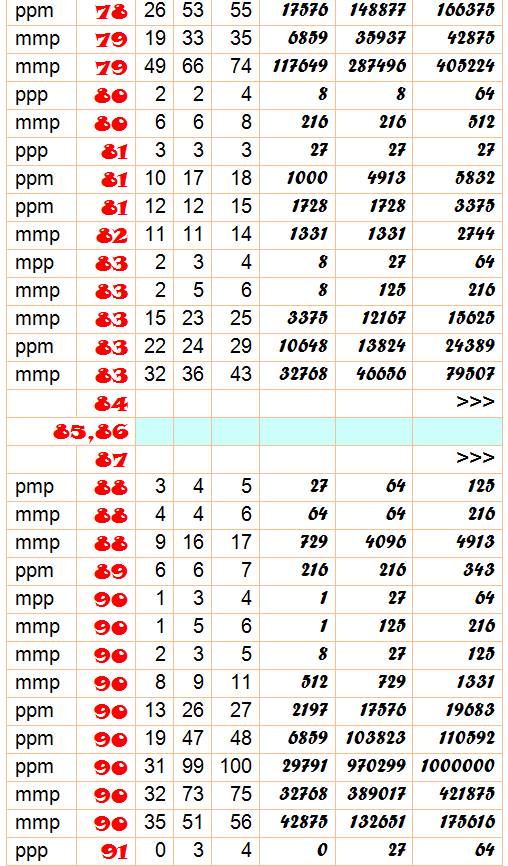
Les récalcitrants: grands nombres ou inconnus
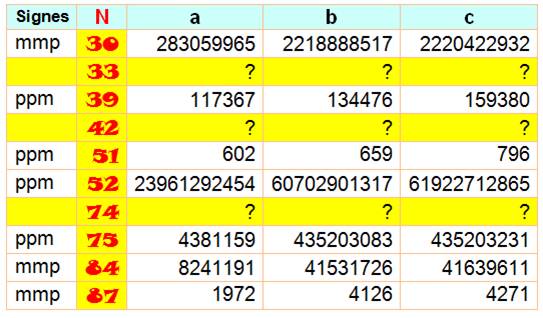
Le cas N = 30 n'a été
trouvé qu'en 1999, par exemple.
Pour 33, 42 et 74, (a,
b, c) > 1014
Voir Tables /
Somme de cubes
TOUS CONNUS jusqu'à 100 en 2019
|
Les
cas 33 et 74 sont désormais connu
(2016 et 2019) Le
cas 42 a été résolu en septembre2019. Le
suivant à craquer est 114. Ils
sont dix jusqu'à 1000: 114, 165, 390, 579, 627, 633, 732, 906, 921 et 975. |
Voir Développements en suite actualisée
et LIEN vers une table complète
jusqu'à 1000
|
|
Voir Repdigits
|
|
||
|
Cube modulo 9
ou en prenant les valeurs
plus proches en négatif:
et leur reste avec division
par 9: |
{0, 1, 2, 3, 4, 5,
6, 7, 8} {0, 1,
8, 27, 64, –64, –27, –8, –1} {0, 1, –1,
0, 1, –1,
0, 1, –1}
|
|
|
Somme de trois cubes modulo 9 Cas extrêmes où les trois
cubes sont tous à -1 ou tous à +1. Un nombre N en 9k + 4 ou en 9k + 5 n'est jamais somme de trois cubes. N = n'est jamais somme de trois
cubes. |
La somme de trois cubes ne donne
jamais –4 ou +4 mod 9. |
|
Retour
/ Voir Cubes mod 9
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette Page |
![]()