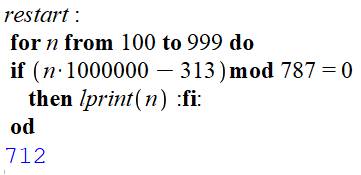NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/03/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	BASES de l'arithmétique
Débutants Nombres	DIVISIONS				Glossaire Division
INDEX CALCUL	Initiation	Avancé	Décimales	Polynôme	Complexes
	Division par 9	Fractions	À l'envers	Division par 90, 99 …
		Sommaire de cette page >>> Ma première division à l'envers >>> Division à l'envers plus complexe >>> Sa solution >>> Résolution avec tableur et programme

DIVISION à l'envers

Comment remonter une division. Sorte de division à trous.

Excellent exercice de maitrise de la division posée.

Énigmes avec nombres choisis.

Propriétés utilisées

1) Les unités d'une multiplication par 7 ont des valeurs différentes selon l'unité du multiplicateur.

2) Choix d'un nombre à diviser avec répétition de 9, proche d'une puissance de 10.

Voir Évaluation de CM1

Ma première division à l'envers
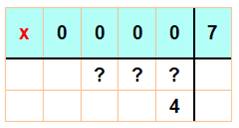
Problème Reconstituer cette division pour trouver la valeur de x, sans calculette. Note: la barre de surlignement indique qu'il faut considérer le nombre complet et non une suite de chiffres.			La division à reconstituer
Principe de la solution L'idée consiste à faire la division en partant du reste; et plus particulièrement du chiffre de ses unités. La théorie La proposition de cette énigme repose sur le fait que les multiples de 0 à 7 du nombre 7 se terminent chacun par un chiffre différent. (0, 7, 14, 21, 28, 35, 42, 49, 56, 63). Alors l'unité du reste induit une unité du multiple de 7 à trouver et donc ce multiple unique.			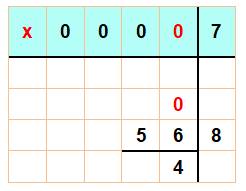La première étape Avec le dernier 0 abaissé et le reste 4, on a 10 – 4 = 6. (10, du fait d'une retenue). Il faut trouver un multiple de 7 qui se termine par 6. Le seul est 8 x 7 = 56.
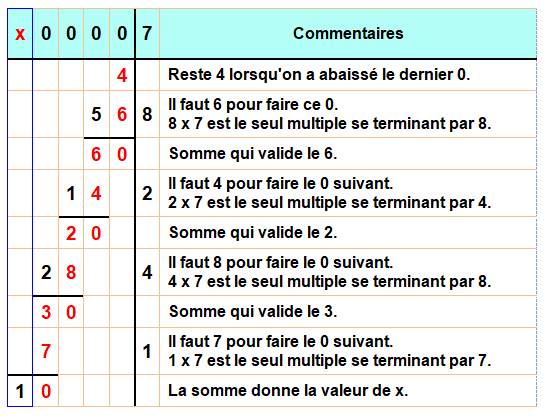
Résolution Comme il s'agit d'une division à l'envers effectuons-la à l'envers. Bilan 10 000 = 1 428 x 7 + 4 9 996 = 1 428 x 7 Nombres propices La configuration avec trois 9, donc proche d'une puissance de 10 est propice à cette énigme.
La même avec un zéro de plus. Trouvez la valeur de x. Voir Les repdigits partiels		Solution 100 000 = 14 285 x 7 + 5 99 995 = 14 285 x 7

Division à l'envers plus complexe
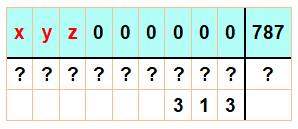
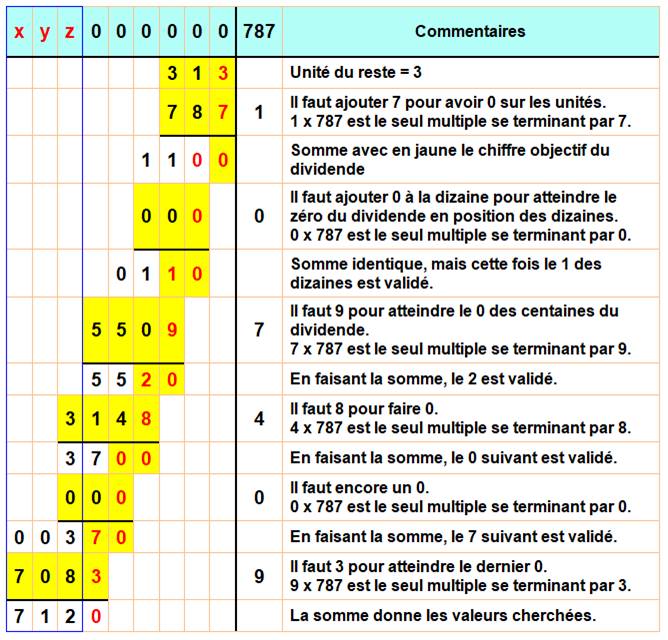
Problème Reconstituer cette division pour trouver la valeur de x, y et z.
Solution 712 000 000 = 904 701 x 787 + 313 711 999 687 = 904 701 x 787

Problème proposé par Tangente n° 108 en janvier-février 2008 – page 46 – Auteur M.R. Parmentier

Résolution avec tableur et programme
Exercice intéressant de familiarisation avec le tableur La quantité de millions (xyz) varie de 100 à 999. Au pire c'est mille lignes de tableur à tirer. La première ligne contient: En B1: le nombre 100 (ici, on a mis 710 pour limiter le tableau); En C1: on forme le nombre B1 x 1000 000 et on calcule le reste de la division par 7 (effet de MOD); et En D1: recherche d'un reste égal à 313 avec l'instruction: =SI(C2=313;"BINGO";" n") Une fois la première ligne écrite Sélectionnez les trois cellules (B1, C1 et D1); Tirez la poignée bas-droite d'un cran vers le bas pour recopier la première ligne en deuxième ligne. Modifiez B2 avec 101(ici, 711). Sélectionnez les six cellules (B1, C1, D1, B2, C2 et D2); Tirez la poignée bas-droite jusqu'à atteindre 999 en colonne B. Repérez où se trouve "BINGO". C'est la solution.		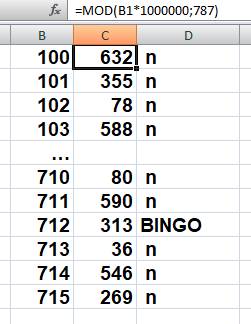Extrait de la page du tableur En bref B1: entrée du nombre 100 C1: =MOD(B1*1000000;787) D1: =SI(C1=313;"BINGO";" n") Copie des lignes jusqu'à 999 BINGO se produit en ligne 712 => xyz = 712
Avec un logiciel, la solution est immédiate
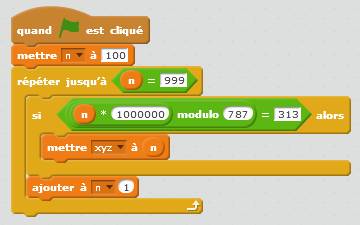
La résolution avec le logiciel gratuit Scratch est tout aussi simple. L'exécution de ce programme montre:

Voir Programmation – Index

Retour	Divisions à plusieurs chiffres
Voir suite en	Division euclidienne (théorie) Méthode Singapour Glossaire – Division La preuve par neuf Repdigits partiels
Voir	Barre magiques des premiers Calcul mental – Index Débutants – Index Fractions Jeux et énigmes – Index Multiplication
Cette page	http://villemin.gerard.free.fr/Calcul/Operatio/DivEnver.htm