NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/11/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Calculs avancés
Débutants Calcul	Exploits humains			Glossaire Opérations
INDEX CALCUL	Prodiges	Carrés	Racine 13^e
		Sommaire de cette page >>> Calculateurs >>> Techniques >>> Inaudi >>> Somme de carrés: trouvez les nombres >>> Shakuntala Devi >>> Lu Chao >>> Daniel Tammet

Calculateurs prodiges

Le calcul mental se perd du fait de l'avènement des calculettes et autres feuilles de calcul. Seul un entraînement régulier permet de faire des calculs de tête ou d'évaluer des ordres de grandeur.

Certains souhaitent aller plus loin et mettent en œuvre des techniques de calculs adaptées au défi qu'ils se posent. Le calcul de la racine treizième en est un.

Anglais: Mental calculators, Lightning calculators, Human computer

Calculateurs

Les calculateurs prodiges sont très rares: Ce sont des personnes naturellement douées qui passent un temps infini à cultiver cette passion. Ce sont aussi certains autismes qui possèdent un don naturel de calcul et de vison des nombres (parfois sous forme de dessins, de couleurs …). Leurs facultés sont concentrées sur ce sujet et sont assez pauvres dans les autres domaines. Ces personnes douées en calcul mental étaient très recherchées dans le passé, avant l'arrivée des ordinateurs, pour établir des tables de nombres (tables de logarithmes, tables trigonométriques …). Il existe une coupe mondiale du calcul mental qui a lieu tous les deux ans.

Techniques

Si les calculateurs prodiges développent des procédés de calcul particuliers, ils sont avant tous dotés d'une mémoire fantastique. Ce sont des mennonistes des chiffres. Ils ont une facilité hors du commun pour mémoriser les résultats intermédiaires. Analogie ordinateurs: ils possèdent une pile de registres impressionnante. Les opérations sont généralement effectuées en commençant par les chiffres de poids forts, donc de gauche à droite et non comme nous l'avons appris à l'école de droite à gauche. Il faut être doué pour se préparer à une propagation des retenues dans les chiffres déjà calculés! Les techniques mnémotechniques sont connues, mais nécessitant une volonté de fer pour les appliquer. Une méthode consiste à ranger les données à mémoriser dans des boites, chacune étant une pièce de votre appartement ou lieux familiers. Les exploits concernent des défis comme: Multiplication de grands nombres, Factorisation de tels nombres, Calcul de carrés, de racines carrées, Calcul de racine cubique, racine treizièmes … Trouver le jour de la semaine d'une date donnée (calendar reckoning), Etc. Certains sont doués d'une mémoire eidétique, mémoire photographique, ou mémoire absolue: capacité de se souvenir d'une grande quantité d'images, de sons, ou d'objets dans leurs moindres détails.

Giacomo Inaudi (1867-1950)

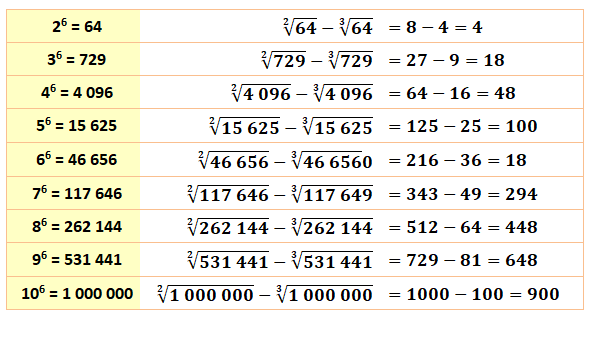
Exceptionnelle mémoire des chiffres, mais sans connaissance particulière des chiffres. Spécialité: trouver quatre nombres consécutifs dont on connait la somme des carrés. Il eut des difficultés à trouver un nombre tel que la différence entre la racine carré et la racine cubique est k = 18 (le seul). On trouve des solutions pour k ayant d'autres valeurs: Les nombres sont à la fois carrés et cubes et donc des puissances sixièmes.

Somme de k carrés – Trouvez les nombres
Formule pour trois carrés (n – 1)² + n² + (n + 1)² = 3n² + 2	Exemple 1 (3, 4, 5) => 3² + 4² + 5² = 50 Retirer 2: 50 – 2 = 48 Diviser par 3: 48 / 3 = 16 (doit être un carré) Sa racine: 16 = 4² Nombres cherchés: 3, 4, 5. Exemple 2 (25, 26, 27) => 24² + 25² + 26² + 27² = 1877 Retirer 2: 1875 Diviser par 3: 625 = 25² Nombres cherchés: 24, 25, 26.
Formule pour quatre carrés (n – 1)² + n² + (n + 1)² + (n + 2)² = 4n² + 4n + 6	Exemple 1 (2, 3, 4, 5) => 2² + 3² + 4² + 5² = 54 Retirer 6: 54 – 6 = 48 Diviser par 4: 48 / 4 = 12 = n² + n = n(n+1) Facteurs consécutifs: 12 = 3 x 4 Nombres cherchés: 2, 3, 4, 5 Exemple 2 (24, 25, 26, 27) => 24² + 25² + 26² + 27² = 2 606 Retirer 6: 2 600 Diviser par 4: 650 Facteurs consécutifs: 25x25 = 625; 25x26 = 650 Nombres cherchés: 24, 25, 26, 27.
Formule pour cinq carrés (n – 2)² + (n – 1)² + n² + (n + 1)² + (n + 2)² = 5n² + 10	Exemple 1 (2, 3, 4, 5, 6) => 2² + 3² + 4² + 5² = 90 Retirer 10: 90 – 10 = 80 Diviser par 5: 8 x 2 / 10 = 16 = 4² Nombres cherchés: 2, 3, 4, 5, 6. Exemple 2 (24, 25, 26, 27, 28) => 24² + 25² + 26² + 27² + 28² = 3 390 Retirer 10: 3 380 Diviser par 5: 3 380 x 2 / 10 = 676 = 26² Nombres cherchés: 24, 24, 26,27, 28.
Formule pour six carrés (n – 2)² + (n – 1)² + n² + (n + 1)² + (n + 2)² + (n + 3)² = 6n² + 6n + 19	Exemple 1 (2, 3, 4, 5, 6, 7) => 2² + 3² + 4² + 5² + 7² = 139 Retirer 19: 139 – 19 = 120 Diviser par 6: 120 / 6 = 20 Facteurs consécutifs: 4 x 5 Nombres cherchés: 2, 3, 4, 5, 6, 7.
Formule pour trois cubes (n – 1)^3 + n^3 + (n + 1)^3 = 3n^3 + 6n	Exemple (3, 4, 5) => 3^3 + 4^3 + 5^3 = 216 Diviser par 3: 216/3 = 72 = n^3 + 6n = n (n² + 2) Facteurs: 72 = 2 x 2 x 2 x 3 x 3 =>72 = 4 x 6² Nombres cherchés: 3, 4, 5.

Voir Somme des carrés des nombres consécutifs

Shakuntala Devi (1939- ) – Femme prodige
1977: elle calcule plus rapidement qu'un ordinateur. Elle calcule aussi : en moins d'une minute. Elle calcule la racine 23^e d'un nombre de 200 chiffres. 1980: elle multiplie deux nombres à treize chiffres choisis au hasard en 28 secondes: 7 686 369 774 870 x 2 465 099 745 779 = 18 947 668 177 995 426 462 773 730.

Lu Chao

Détenteur du record de mémorisation des décimales de Pi depuis 2006. 67 890 décimales récitées en 24 heures et 4 minutes. Un an de travail de mémorisation! Il avait 24 ans. Capable de mémoriser 100 chiffres en 10 minutes. Pour son exploit, il a dû enregistrer une moyenne de 200 chiffres par jour. Il visait les 100 000 mais s'est trompé à la 67 890^e. Il a énoncé 5 au lieu de 0. Précédent record: 42 195 décimales par un Japonais. Lu Chao s'est lancé se défie pour attirer l'attention sur le fait que c'est un Chinois ancien, Zu Chonzhi, qui a découvert le ratio entre la circonférence et le diamètre d'un cercle.

Daniel TAMMET (1979-)

Écrivain, poète et linguiste anglais atteint du syndrome d'Asperger. Sait donner le jour de la semaine en un éclair. En 2004, il met un peu plus de 5 heures pour réciter 22 514 décimales de Pi, apprises en 3 mois. L'Homme ordinateur est un documentaire qui lui est consacré. Il apprend l'islandais en une semaine et se prête avec succès à une interview dans cette langue. En 2012, il a déjà publié trois livres, dont sa biographie. Je suis né un jour bleu (autobiographie), Embrassez le ciel immense, L'éternité dans une heure – La poésie des nombres

Suite	Calcul mental des carrés Calcul mental – Index
Voir	Arithmétique – Glossaire Calcul des carrés Carré magique Jeux – Index Logarithmes Moyennes Multiplications védiques QI Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/Calcul/Prodige.htm