|
||||||||||||||||||||||||||||||
![]()
|
DÉNOMBRER
– Les BASES Méthodes
essentielles Dénombrer une collection d'objets, c'est
déterminer la quantité d'éléments de cet ensemble, soit par un comptage direct, soit par un calcul à l'aide de techniques
particulières, dites combinatoires. Quelles sont les principales méthodes pour dénombrer
des objets ?
|
Un brin de
théorie
|
|
||
|
Les cinq
principes du comptage:
|
Pour compter, on assigne un numéro à chacun
des objets:
|
|
Voir Cardinal et ordinal
Les
méthodes de dénombrement
|
|
|||
|
Chloé
dispose de quatre pantalons et trois chemises. Combien
de tenues possibles ? |
Nommons A, B, C et D les pantalons et 1, 2, 3,
les chemises. Énumérons les possibilités: A1, A2, A3, B1, B2,
B3, C1, C2, C3, D1, D2 D3 Bilan: 4 x 3 = 12 tenues possibles. Voir Produit
cartésien |
||
|
On
dispose de 10 balles numérotées de 1 à 10 et d'un support de 10 trous. Combien
de dispositions possibles ? |
Dans le premier trou, on choisit une balle parmi
10. Dans le deuxième trou, on place une balle parmi
les 9 qui restent. Une parmi les 8 qui restent dans le troisième
trou; etc. Bilan: 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 =
10! = 3 628 800 Voir Factorielle |
||
|
Combien
de carrés dans ce quadrillage ? Dénombrement par comptage
Bilan: 1 + 4 + 9 + 16 + 25 + 36 = 6 x 7 x 13 / 6 = 91 Voir
Somme
des carrés / Brève
n°383 / Carrés dans le carré |
|
||
|
|
||
|
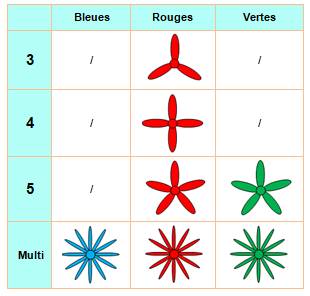
On fait
un herbier avec des fleurs bleues, rouges ou vertes. Elles ont 3, 4, 5 ou de
multiples pétales. Les
fleurs bleues sont toujours multi-pétales et il n'y a pas de fleurs vertes à
3 ou 4 pétales. Combien
de possibilités ? Le tableau à double entrée montre qu'il y a sept
possibilités de fleurs sur un total de 3 x 4 = 12 possibilités. Il est parfois plus facile de compter ce qu'il
n'y a pas: ici 3 bleues et 2 vertes = 5 fleurs inexistantes. |
|
|
|
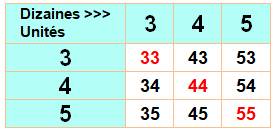
Combien
de nombres de deux chiffres peut-on écrire avec les chiffres 3, 4 et 5 ? Le tableau à double entrée montre qu'il y a 3 x
3 = 9 nombres à deux chiffres formés avec
les chiffres 3, 4 et 5; dont 6 seulement sont différents (rouges). |
|
|
|
|
||
|
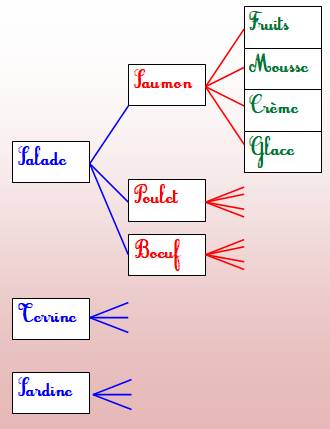
On se
propose de connaitre la quantité de choix de repas possibles à partir d'une
carte suivante:
L'arbre de choix montre les diverses
possibilités: Ayant choisi la salade puis le saumon, on a
encore le choix entre quatre desserts. Ayant choisi le poulet, encore quatre desserts;
et idem pour le choix du bœuf. Avec la salade, on trouve 3 x 4 = 12
possibilités. En choisissant la terrine, même jeu de
possibilités et idem avec la sardine. Finalement, il y a 3 x 12 = 36 possibilités de
types de repas avec cette carte de menus. Avec l'habitude, le dessin de l'arbre devient
inutile. |
|
|
|
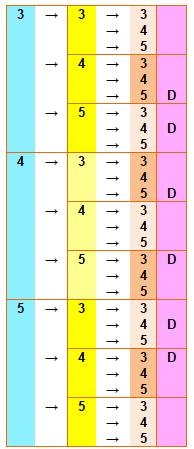
Combien
de nombres de trois chiffres peut-on écrire avec les chiffres 3, 4 et 5 ? Chiffres quelconques L'arbre de choix ci-contre montre les 27 possibilités. Ici, le dénombrement semble assez facile:
Bilan: 3 x 3 x 3 = 27 possibilités. Chiffres tous différents On repère avec un D dans la colonne de droite les
cas où les chiffres sont tous différents. Il y en a six. Un simple raisonnement permet de les dénombrer: après avec choisi un nombre parmi trois pour les
centaines, il ne reste plus que deux possibilités pour les dizaines et,
finalement, le chiffre des unités est imposé par la chiffre qui reste. Bilan: 3 x 2 = 6 nombres de trois chiffres avec
des chiffres différents. |
|
|
|
|
||
|
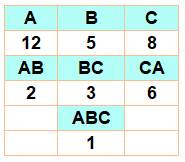
Problème Examen
avec trois matières: Algèbre, Biologie et Chimie pour 41 étudiants. Le
tableau indique les non-reçus selon la ou les matières:
Combien
sont-ils à avoir échoué dans une matière au moins ? Commentaires Le diagramme de Venn est
ici complètement résolu et il donne bien d'autres renseignements: Avec 41 candidats, si 15 ont échoué quelque part,
il y en a 26 qui ont réussi dans les trois matières à la fois. Si quelqu'un a échoué en chimie, il a aussi
manqué une autre matière (C seul = 0) Il y a 3 personnes qui on réussi l'algèbre sans
réussir la chimie et la biologie (zone de B et C sans A => 1 + 2 + 0 = 3) |
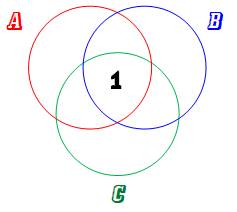
Résolution en
trois temps Trois zones (ici des cercles) représentent les
échecs dans chacune des disciplines. De manière évidente, on peut dire que
l'intersection ABC contient un individu.
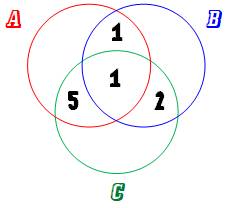
Parmi les 2 qui ont échoué en AB, un a aussi
échoué en ABC; reste un seul individu qui a échoué en AB seulement. Même
raisonnement pour AC en propre: 3 – 1 = 2 et pour BC: 6 – 1 = 5.
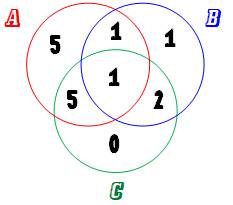
Parmi les 12 qui ont échoué en A, 5 + 1 + 1 ont
aussi échoué ailleurs. Reste: 12 – 7 = 5 qui ont échoué en A seulement. Pour
B: 5 – 4 = 1 et pour C: 8 – 8 = 0.
Bilan: 5 + 1 + 1 + 1 + 5 + 2 + 0 = 15 personnes ont échoué à au moins une matière
(somme des nombres dans les cercles). |
|
|
|
||
|
Combien
de nombres de quatre chiffres peut-on écrire avec tous des chiffres de 0 à 9
? Combien
de nombres de quatre chiffres avec des chiffres tous différents ? |
Chiffres quelconques
Bilan : 10 x 10 x 10 x 9 = 9 000 nombres de quatre chiffres. Chiffres tous différents
Bilan: 9 x 9 x 8 x 7 = 4 536 nombres de quatre chiffres avec chiffres
différents. |
|
Voir DicoNombre
4 536
|
Combien de "1" dans tous les nombres de
0 à 999 ? |
Bilan: 100 + 100 + 100 = 300 fois le "1" dans les nombres de 0 à 999. Note: un décompte semblable donnerait 190 fois le "0".
|
|
Combien de nombres de quatre chiffres comporte un
"0" ? |
On pourrait faire le décompte général:
Un raisonnement évite ce décompte fastidieux: D'abord, il ne faut pas compter les "0" car avec 1000, on compterait
ce nombre trois fois. Comment s'en sortir ? L'astuce, souvent employée, consiste à compter les nombres sans
"0". Parmi les 9 000 (9 999 – 999) nombres à quatre chiffres, on choisit le
chiffre des milliers (1 parmi 9, sans le "0"); le chiffre des
centaines (1 parmi 8, sans le "0", ni celui déjà choisi); etc. Bilan: 9 x 9 x 9 x 9 = 6 561 nombres de quatre chiffres sans le
"0". Soit: 9 000 – 6 561 = 2 439 nombres de quatre chiffres avec le "0". |
|
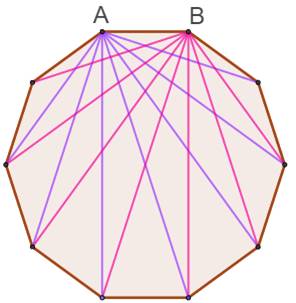
Soit 10
points non alignés, combien peut-on former de segments ? Une illustration aide au raisonnement:
Bilan: 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 Voir
Somme des
entiers |
|
|
|
Combien
de rectangles dans ce quadrillage ? Dénombrement par comptage
Dénombrement par raisonnement Les rectangles sont formés par un couple de
droites horizontales non confondues et un couple de droites verticales non
confondues.
Bilan: 21 x 21 = 441 rectangles |
Note: Pour ceux
qui voudraient poursuivre le décompte par comptage: 91 + 2x6 (5+4+2+1) + 2x5
(3+4+2+1) |
|
|
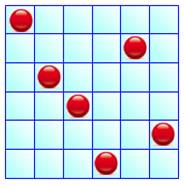
Sur cette
grille, on souhaite placer six pions tels que sur chaque ligne et sur chaque
colonne, il n'y ait qu'un seul pion. Combien
de possibilités ? Dénombrement par raisonnement Choix de 1 position parmi 6 sur la colonne de
gauche; Choix de 1 position parmi 5 sur la colonne
suivante; Etc. Bilan: 6 x 5 x 4 x 3 x 2 x1 = 6! = 720
dispositions différentes. |
|
|
Pour aller plus loin
|
Les cas exposés ici sont
simples. Rapidement vous serez confronté à des cas plus délicats. Les outils
à connaitre seront:
|
![]()
|
Suite |
|
|
Retour |
|
|
Je débute |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()