|
|||||||||||||||||||||||||||||||||||
![]()
|
À
QUATRE autour d'une TABLE RONDE Combien de possibilités pour
disposer les convives. |
En résumé
|
Quantité
de dispositions avec k convives (k personnes):
|
|
|
||
|
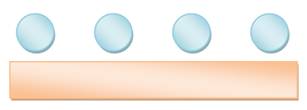
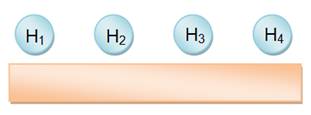
Table en
ligne (banc ou table en U)
4
! se lit factorielle 4. |
N = 4 ! = 24 Voici les 24
arrangements ABCD BACD CABD DABC ABDC BADC CADB DACB ACBD BCAD CBAD DBAC ACDB BCDA CBDA DBCA ADBC BDAC CDAB DCAB ADCB BDCA CDBA DCBA |
|
|
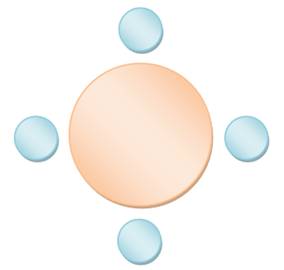
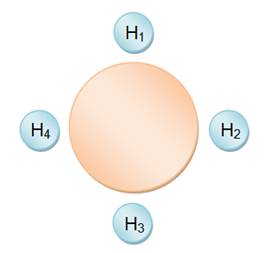
Table en
rond
|
N = 4! / 4 = 3 ! = 6 Voici les 6 arrangements qui subsistent ABCD ABDC ACBD ACDB ADBC ADCB |
|
|
|
||
|
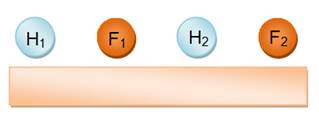
Table en
ligne
|
H1 F1 H2 F2 H1 F2 H2 F1 H2 F1 H1 F2 H2 F2 H1 F1 N = 4 |
|
|
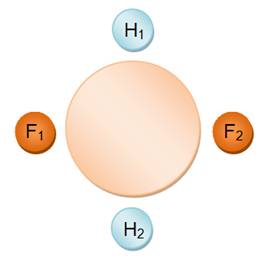
Table en
rond
|
N = 1 |
|
|
|
||
|
Table en
ligne
|
12 213
324 43 123 3124 / 2134
423 124 3124 1 2 3 4 & 2 4 1 3 N = 2 |
|
|
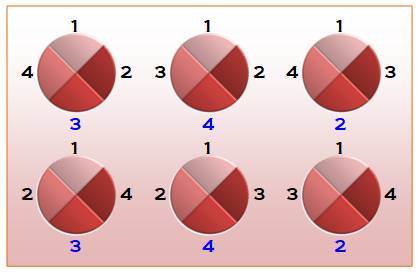
Table en
rond
|
1 2 3 4 N = 1 |
|
|
S'en
persuader!
|
Toutes les
permutations – Table en ligne [1,
2, 3, 4], [1, 2, 4, 3], [1, 3, 2, 4], [1, 3, 4, 2], [1, 4, 2, 3], [1, 4, 3, 2], [2, 1, 3, 4], [2, 1, 4, 3], [2, 3, 1, 4], [2, 3, 4, 1], [2, 4, 1, 3], [2, 4, 3, 1], [3, 1, 2, 4], [3, 1, 4, 2], [3, 2, 1, 4], [3, 2, 4, 1], [3, 4, 1, 2], [3, 4, 2, 1], [4, 1, 2, 3], [4, 1, 3, 2], [4, 2, 1, 3], [4, 2, 3, 1], [4, 3, 1, 2], [4, 3, 2, 1] Permutations sans
voisinage avec distance unité [1, 2, 3, 4], [2, 4, 1, 3], [3, 1, 4, 2] Permutations sans
voisinage du tout [1, 2, 3, 4], [2, 4, 1, 3], |
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()