Autour d'une table ronde à cinq

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/01/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Dénombrement
Débutants Dénombrement	Autour d'une TABLE RONDE				Glossaire Combinatoire
INDEX Dénombrement	3 personnes	4 personnes	5 personnes	6 personnes
		Sommaire de cette page >>> 5 personnes (libres) >>> 5 personnes en couples >>> 5 personnes voisines une seule fois >>> Jamais le même couple de voisins

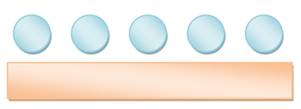
À CINQ autour d'une TABLE RONDE

Combien de possibilités pour disposer les convives.

Anglais: The Dinner Table Problem

En résumé

Quantité de dispositions avec k convives (k personnes):

Sur un banc (ou table en ligne): k! = 1 x 2 x 3 … x k

Autour d'un table ronde: (k – 1)! = 1 x 2 x 3 … x (k – 1)

5 personnes (libres)
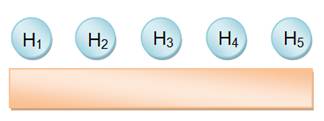
Table en ligne (banc ou table en U) Cinq convives. Combien de repas pour couvrir toutes les possibilités de placements de ces convives le long de la table? C'est un arrangement: Je choisis le premier: 5 possibilités; Je choisis le deuxième: 4 possibilités; Etc. Soit 5 x 4 x 3 x 2 x 1 = 5! = 120 5 ! se lit factorielle 5.	N = 5 ! = 120
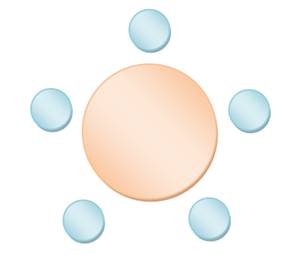
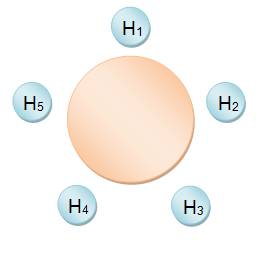
Table en rond Cinq convives. Combien de repas pour couvrir toutes les possibilités de placements de ces convives le long de la table? C'est un arrangement particulier! Le premier convive, par exemple, peut être placé n'importe où sans changer ses conditions de son voisinage. Seule change sa situation géographique dans la pièce; Il s'agit de la quantité d'arrangements hors permutations circulaires.	N = 5! / 5 = 4 ! = 24

5 personnes en couples

Table en ligne

Cinq convives: 3 hommes et deux femmes.

Combien de possibilités en conservant l'alternance homme-femme?

C'est un arrangement très particulier:

Voyons les cas possibles;

On permute les femmes ou on permute les hommes;

Soit 12 possibilités.

H₁ F₁ H₂ F₂ H₃

H₁ F₂ H₂ F₁ H₃

H₁ F₁ H₃ F₂ H₂

H₁ F₂ H₃ F₁ H₂

H₂ F₁ H₁ F₂ H₃

H₂ F₂ H₁ F₁ H₃

H₂ F₁ H₃ F₂ H₁

H₂ F₂ H₃ F₁ H₁

H₃ F₁ H₁ F₂ H₂

H₃ F₂ H₁ F₁ H₂

H₃ F₁ H₂ F₂ H₁

H₃ F₂ H₂ F₁ H₁

N = 12

Table en rond

Cinq convives: 3 hommes et deux femmes.

Combien de possibilités en conservant l'alternance homme-femme?

Le cas est peu intéressant du fait qu'il n'y a pas un nombre exact de couple;

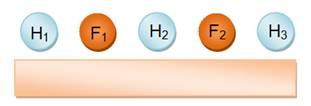
La quantité d'arrangements est la même que pour la table en ligne.

N = 12

5 personnes voisines une seule fois
L'idée ici est de compter combien de déjeuners SUCCESSIFS on peut organiser. Table en ligne Cinq convives. Combien de possibilités de placements sachant que chaque ne peut avoir le même voisin qu'une seule fois? C'est un arrangement très particulier: Voyons les cas possibles; Pour s'y retrouver, on note en exposant les voisins déjà rencontré par la personne; Par exemple: 2¹³ signifie que la personne n°2 a déjà eu comme voisines les personnes 1 et 3; par conséquent, on ne peut plus mettre ces personnes à côté de lui.		1² 2¹³ 3²⁴ 4³⁵ 5⁴ 1²³ 3¹²⁴⁵ 5²³⁴ 2¹³⁴⁵ 4²³⁵ 1²³ 4¹²³⁵ / 1²³ 5¹²³⁴ / 5²³⁴ 1²³ 4²³⁵ / 1 2 3 4 5 & 1 3 5 2 4 N = 2
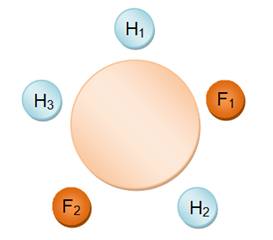
Table en rond Cinq convives. Combien de possibilités de placements sachant que chaque ne peut avoir le même voisin qu'une seule fois? C'est le même cas que précédemment en retirant les cas supplémentaires de proximité de 1 avec 5. Parmi les deux solutions que nous avions trouvées ce cas ne se présente pas.		1 2 3 4 5 et 1 3 5 2 4 N = 2
S'en persuader! Parmi les 120 arrangements, il est curieux de n'avoir que si peu de cas d'arrangements avec voisins uniques. Un premier tri consiste à éliminer tous ceux pour lesquels on retrouve une distance de voisinage égale à 1. Cas de 1 et 2, 2 et 3, 3 et 4 & 4 et 5. De 120, on passe à 15 seulement. On repère en rouge les voisinages déjà existants dans la deuxième permutation pour éliminer ces cas.	Toutes les permutations – Table en ligne [1, 2, 3, 4, 5], [1, 2, 3, 5, 4], [1, 2, 4, 3, 5], [1, 2, 4, 5, 3], [1, 2, 5, 3, 4], [1, 2, 5, 4, 3], [1, 3, 2, 4, 5], [1, 3, 2, 5, 4], [1, 3, 4, 2, 5], [1, 3, 4, 5, 2], [1, 3, 5, 2, 4], [1, 3, 5, 4, 2], [1, 4, 2, 3, 5], [1, 4, 2, 5, 3], [1, 4, 3, 2, 5], [1, 4, 3, 5, 2], [1, 4, 5, 2, 3], [1, 4, 5, 3, 2], [1, 5, 2, 3, 4], [1, 5, 2, 4, 3], [1, 5, 3, 2, 4], [1, 5, 3, 4, 2], [1, 5, 4, 2, 3], [1, 5, 4, 3, 2], [2, 1, 3, 4, 5], [2, 1, 3, 5, 4], [2, 1, 4, 3, 5], [2, 1, 4, 5, 3], [2, 1, 5, 3, 4], [2, 1, 5, 4, 3], [2, 3, 1, 4, 5], [2, 3, 1, 5, 4], [2, 3, 4, 1, 5], [2, 3, 4, 5, 1], [2, 3, 5, 1, 4], [2, 3, 5, 4, 1], [2, 4, 1, 3, 5], [2, 4, 1, 5, 3], [2, 4, 3, 1, 5], [2, 4, 3, 5, 1], [2, 4, 5, 1, 3], [2, 4, 5, 3, 1], [2, 5, 1, 3, 4], [2, 5, 1, 4, 3], [2, 5, 3, 1, 4], [2, 5, 3, 4, 1], [2, 5, 4, 1, 3], [2, 5, 4, 3, 1], [3, 1, 2, 4, 5], [3, 1, 2, 5, 4], [3, 1, 4, 2, 5], [3, 1, 4, 5, 2], [3, 1, 5, 2, 4], [3, 1, 5, 4, 2], [3, 2, 1, 4, 5], [3, 2, 1, 5, 4], [3, 2, 4, 1, 5], [3, 2, 4, 5, 1], [3, 2, 5, 1, 4], [3, 2, 5, 4, 1], [3, 4, 1, 2, 5], [3, 4, 1, 5, 2], [3, 4, 2, 1, 5], [3, 4, 2, 5, 1], [3, 4, 5, 1, 2], [3, 4, 5, 2, 1], [3, 5, 1, 2, 4], [3, 5, 1, 4, 2], [3, 5, 2, 1, 4], [3, 5, 2, 4, 1], [3, 5, 4, 1, 2], [3, 5, 4, 2, 1], [4, 1, 2, 3, 5], [4, 1, 2, 5, 3], [4, 1, 3, 2, 5], [4, 1, 3, 5, 2], [4, 1, 5, 2, 3], [4, 1, 5, 3, 2], [4, 2, 1, 3, 5], [4, 2, 1, 5, 3], [4, 2, 3, 1, 5], [4, 2, 3, 5, 1], [4, 2, 5, 1, 3], [4, 2, 5, 3, 1], [4, 3, 1, 2, 5], [4, 3, 1, 5, 2], [4, 3, 2, 1, 5], [4, 3, 2, 5, 1], [4, 3, 5, 1, 2], [4, 3, 5, 2, 1], [4, 5, 1, 2, 3], [4, 5, 1, 3, 2], [4, 5, 2, 1, 3], [4, 5, 2, 3, 1], [4, 5, 3, 1, 2], [4, 5, 3, 2, 1], [5, 1, 2, 3, 4], [5, 1, 2, 4, 3], [5, 1, 3, 2, 4], [5, 1, 3, 4, 2], [5, 1, 4, 2, 3], [5, 1, 4, 3, 2], [5, 2, 1, 3, 4], [5, 2, 1, 4, 3], [5, 2, 3, 1, 4], [5, 2, 3, 4, 1], [5, 2, 4, 1, 3], [5, 2, 4, 3, 1], [5, 3, 1, 2, 4], [5, 3, 1, 4, 2], [5, 3, 2, 1, 4], [5, 3, 2, 4, 1], [5, 3, 4, 1, 2], [5, 3, 4, 2, 1], [5, 4, 1, 2, 3], [5, 4, 1, 3, 2], [5, 4, 2, 1, 3], [5, 4, 2, 3, 1], [5, 4, 3, 1, 2], [5, 4, 3, 2, 1] Permutations sans voisinage avec distance unité [1, 2, 3, 4, 5], [1, 3, 5, 2, 4], [1, 4, 2, 5, 3], [2, 4, 1, 3, 5], [2, 4, 1, 5, 3], [2, 5, 3, 1, 4], [3, 1, 4, 2, 5], [3, 1, 5, 2, 4], [3, 5, 1, 4, 2], [3, 5, 2, 4, 1], [4, 1, 3, 5, 2], [4, 2, 5, 1, 3], [4, 2, 5, 3, 1], [5, 2, 4, 1, 3], [5, 3, 1, 4, 2] Permutations sans voisinage du tout [1, 2, 3, 4, 5], [1, 3, 5, 2, 4]

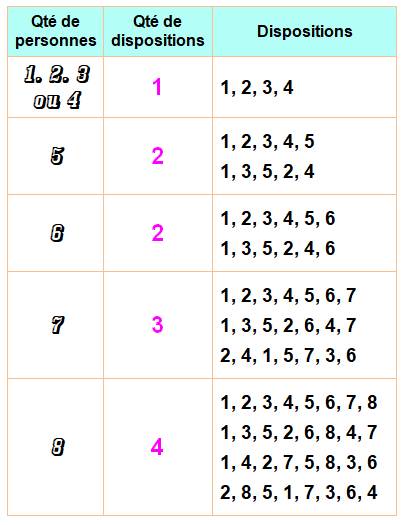
Avec plus de personnes

Les mêmes méthodes montrent qu'avec six personnes permutées le long d'un banc, il n'existe que deux possibilités pour les disposer de façon telle qu'elles n'aient jamais le même voisin.

1, 2, 3, 4, 5, 6 & 1, 3, 5, 2, 4, 6.

Récapitulatif de 1 à 8 personnes sur un banc

sans jamais avoir la même personne comme voisin

Autour d'une table ronde, on retrouve ces dispositions et leurs dispositions symétriques (en lisant les nombres de droite à gauche).

Jamais le même couple de voisins

L'idée ici est de compter combien il y a de possibilités d'organiser un SECOND déjeuner sans qu'une personne ne retrouve LES DEUX mêmes voisins.

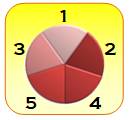
Premier déjeuner – Référence

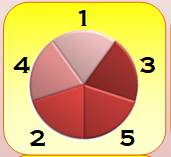
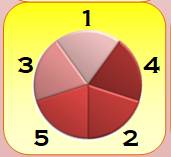
Second déjeuner

Placement correct

Le 1 ne retrouve pas le 2 et le 5 à la fois.

Le 2 ne retrouve pas le 1 et le 3 à la fois.

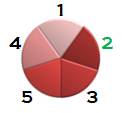
Seconde déjeuner

Placement incorrect

Le 2 retrouve le 1 ET le 3 une nouvelle fois.

Mon décompte (ci-dessous) pour cinq personnes montre qu'il y a douze possibilités pour organiser le second déjeuner sans qu'une personne ne retrouve à la fois les deux mêmes voisins.

En réalité, la moitié, si on exclut les configurations symétriques (lignes 2 et 4 sur le tableau ci-dessous).

L'encyclopédie des suites de nombres indique dix.

A089222 – Number of ways of sitting n people around a table for the second time without anyone sitting next to the same person as they did the first time : 0, 0, 0, 0, 10, 36, 322, 2 832, 27 954, 299 260 …

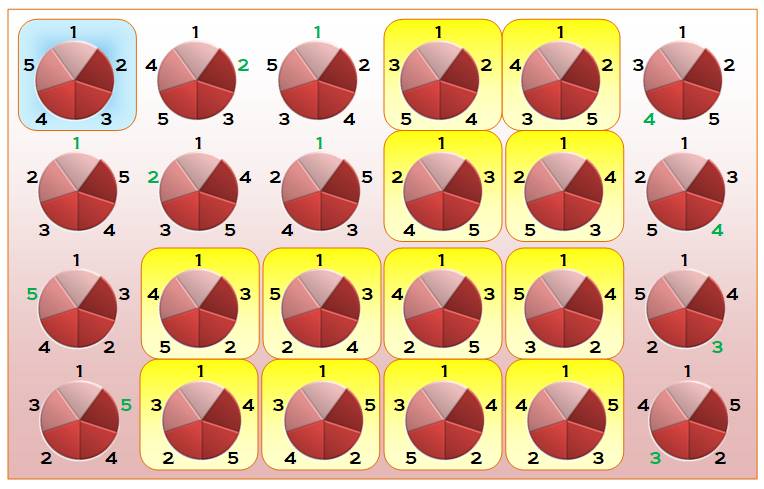
Si quelqu'un détecte pourquoi cette différence, je suis preneur.

ILLUSTRATION – Décompte pour cinq personnes

Les 4! = 24 possibilités. Ligne 2 et 4 les symétriques de 1 et 3.

En bleu le premier déjeuner. En jaune, les douze possibilités pour un second déjeuner.

En vert, le convive qui retrouve les deux mêmes voisins que lors du premier dejeuner.

Pour information

Si on exige qu'une personne ne revoie jamais le même convive comme voisin, il y a une seule possibilité de disposition; ou deux avec sa disposition symétrique.

Suite	Énigme à six autour d'une table
Voir	Combinatoire Combinatoire – Panorama Organisation de tournois Quantité de personnes qui se connaissent Réseaux d'amis – Le petit monde Rondes sociales
Aussi	Dénombrer – Index Compter
Cette page	http://villemin.gerard.free.fr/Denombre/aaaTable/Table5.htm