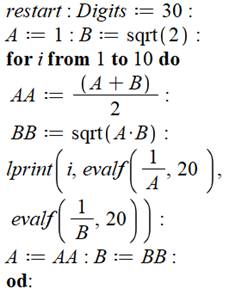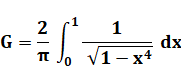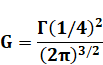|
|||||||||||||||||||||||||||||||||||
![]()
|
|
||||||||||||||||||||||||||||||||||||
|
Définition
Les deux suites, l'une
impliquant la moyenne arithmétique et l'autre la moyenne géométrique,
convergent vers la valeur la valeur limite L. Utilisée en géométrie:
calcul du périmètre de l'ellipse. Départ
Démonstration
Itération (idée de Legendre et Gauss)
Exemples
|
||||||||||||||||||||||||||||||||||||
|
|
|||
|
Définition |
Moyenne
arithmético-géométrique de 1 et de la |
||
|
Constante de Gauss (G) L1 est la première constante de la lemniscate. L2 est la deuxième. U est la constante omniprésente (ubiquitous
constant). |
G = 0,83462684167407318624… M = 1/G = 1,1981402347355922075… L1 = Pi.G = Pi / M =
2,6220575542921198104… L2
= M/2 = 0,59907011736779610376… U
= M / |
||
|
|
Programme de calcul de la
constante Réinitialisation et demande de calculs
avec 30 chiffres. Initialisation des deux valeurs de départ. Boucle de calcul avec 10 itérations Calcul des deux moyennes mise dans des
variables temporaires. Le calcul de BB doit se faire avec A et non la
nouvelle valeur BB. Impression des deux valeurs de G = 1/ A ou
1/B. Mise à jour de A et B avec les nouvelles
valeurs. Voir Programmation – Index |
||
|
1, 1; 0,70710678118654752440 2, 0,82842712474619009760; 0,84089641525371454305 3, 0,83461519927772999779; 0,83463848431402505476 4, 0,83462684163347173961; 0,83462684171467463295 5, 0,83462684167407318631; 0,83462684167407318624 6, 0,83462684167407318624; 0,83462684167407318624 |
Résultat du calcul par
programme Avec six itérations seulement les deux
valeurs convergent avec 20 décimales. |
||
|
Calcul par
intégrale Intégrale trouvée par Gauss en 1799. Cette constante est transcendantale. Expression de G en fonction de Gamma. Constante qui intervient dans le calcul. |
|
||
|
Note: G est
proche du cosinus hyperbolique du nombre
d'or. |
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()