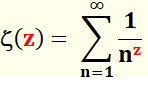NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/11/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres premiers
Débutants Identité d'Euler	Répartition			Glossaire Nombres premiers
Index des pages Nombres premiers >>> INDEX	En bref	Identité d'Euler	Hypothèse de Riemann
	Débutant	Fonction zêta d'Euler	Zêta de Riemann
	Démo. de l'identité	Approches modernes	Fonction de Möbius
	Sommaire de cette page >>> Fonction de Riemann >>> Zéros >>> Historique >>> Conjecture des zéros de Landau-Siegel.

L'hypothèse de Riemann est la longitude des mathématiques. En la résolvant, on ouvre la perspective d'établir la carte des eaux brumeuses du vaste océan des nombres. Cela ne constituerait qu'une étape dans notre compréhension de ce secret de la Nature. Si seulement nous pouvions trouver le secret nous permettant de naviguer sur les nombres premiers, qui sait alors ce que nous trouverions au-delà, n'attendant que nous ?

Marcus du Sautoy

Voir Pensées & humour / Citations mathématiques

HYPOTHÈSE DE RIEMANN

Conjecture de Riemann

Conjecture des zéros de Landau-Siegel

Une conjecture relativement simple, émise en 1859, il y a 150 ans et qui, depuis, résiste aux plus chevronnées des mathématiciens.

Une rage sans pareille pour la démontrer car elle est sans doute la clé du mystère de la répartition des nombres premiers.

Le Graal des mathématiciens ?

On la nomme hypothèse de Riemann, plutôt que conjecture, pour signifier que l'on se situe au-delà de la simple "devinette" mathématique.

En bref

Publiée en 1859, l'hypothèse de Reimann tente de prédire l'occurrence des nombres premiers à l'aide d'une fonction mathématique. L'apparition des nombres premiers ne suit pas un modèle. Après en avoir trouvé un, il est impossible de prédire l'apparition du suivant. Les grands mathématiciens comme Euclide, Euler et Gauss sont parmi ceux qui ont tenté de résoudre ce problème. Bernhard Riemann, un élève de Gauss, a découvert un modèle représentant la fréquence des nombres premiers. Il a constaté qu'ils suivaient un schéma qui pouvait être expliqué par une fonction, qu'il a appelée fonction zêta de Riemann.

Published in 1859, Reimann Hypothesis attempts to predict the occurrence of prime numbers using a mathematical function. Prime numbers do not follow a pattern of occurrence. After you find one, it is impossible to predict the occurrence of the next prime number. Mathematical greats like Euclid, Euler, and Gauss are among many who attempted to address this problem. Bernhard Riemann, a student of Gauss, found a pattern in the frequency of prime numbers. He found them to follow a pattern that could be explained with a function, which he called Riemann zeta function.

Voir Anglais pour le bac et pour les affaires

FONCTION DE RIEMANN

Formulation L'étude de la fonction zêta complexe de Riemann montre qu'elle passe par la valeur zéro. Il existe: des zéros triviaux (sans intérêt) comme -2, -4, -6 … et, des zéros particuliers qui semblent s'aligner sur la droite des réels ½. L'hypothèse ou conjecture de Riemann consiste à affirmer que tous les zéros non triviaux sont sur cette droite ½. Note La relation entre zêta et la distribution des nombres premiers n'est pas évidente. Elle nécessite l'introduction d'une fonction un peu complexe dite de Tchebychev. Cette fonction à base de logarithmes donne approximativement la quantité de premiers et de leurs puissances inférieures à n.

ZÉROS
Non prouvée Tous les zéros sont sur la droite 1/2 Le premier se trouve en 1/2 + i . 14,13… Toutes les valeurs imaginaires sont irrationnelles. Prouvé Tous les zéros sont situés dans une bande critique entre les parties réelles 0 et 1 (bande bleue). En 1896, Hadamard et la Vallée Poussin indépendamment donnent une démonstration du théorème des nombres premiers. Ils utilisent et avaient démontré que la droite 1 ne possède aucun zéro. Les zéros sont symétriques par rapport à la droite 1/2, la droite critique. Il existe une infinité de réels sur cette droite – Prouvé par Godfrey Hardy en 1915. Au moins 1/3 des zéros sont sur cette droite. En 1986, les calculs ont donnés plus de 1 500 000 zéros, tous situés sur la droite ½. Aujourd'hui, le milliard est dépassé La vallée-Poussin en 1896, a trouvé toute une zone de la bande critique sans zéro (surface jaune)
D’autre part, Hardy et Littlewood avait démontré dans les années 1920 une région sans zéro de la forme sigma >1 – k ln ln t / ln t Et Vinogradov, dans les années trente, avait obtenu une région sans zéro de la forme sigma > 1 – k / (ln t)^3/4 Merci à Claude P.

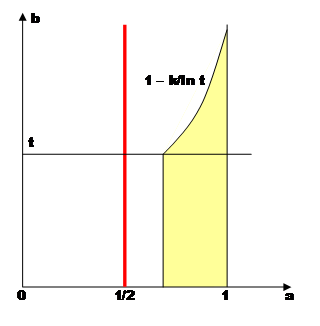
Anglais: Critical line and critical strip

HISTORIQUE

Fonctions spéciales  La fonction zêta joue un rôle important en recherches mathématiques. Elle constitue un premier lien entre arithmétique et analyse. Elle a été utilisée par Euler, Dirichlet, Tchebychev et Riemann pour étudier la distribution des nombres premiers. La fonction zêta de Riemann et les fonctions L de Dirichlet sont des outils analytiques puissants pour étudier la répartition des nombres premiers. Il semble que ces fonctions soient aussi révélatrices des propriétés les plus cachées de la théorie des nombres. Elles sont loin d'être bien comprises! En 1737 Leonhard Euler (1707-1783) étudie la fonction zêta et découvre l'identité d'Euler entre les nombres premiers et les nombres entiers. En 1859 Georg Riemann (1826-1866) émet son hypothèse. (Même année que la publication par Darwin sur l'origine des espèces). En 1900 David Hilbert (1862-1943) place l'hypothèse de Riemann parmi les grands défis mathématiques du XX^e siècle (n°8). Depuis 1920, La théorie des nombres et la géométrie algébrique tendent à être unifiées. Ces fonctions ne sont peut être que les éléments fragmentaires d'une théorie plus générale à découvrir. Dedekind a généralisé ces fonctions et relations aux idéaux entiers et idéaux premiers. En1927 L'Allemand Edmund Landau a supposé la conjecture de Riemann vraie, et a montré qu'un grand nombre de conclusions en seraient tirées. En 1935 Une centaine de zéros sont connus grâce au calcul automatique: E. Titchmarsh. Puis rapidement, on en connaît des milliers. 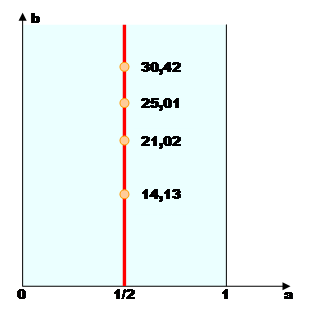Pourcentage sur la droite critique En 1942, Selberg Il démontre qu'au moins une certaine fraction de zéros est sur la droite ½. Mais sa fraction est inférieure à 1%. En 1974, Norman Levinson Il fait passer cette fraction à 1/3. En 1989, Conrey Il la fait monter à 40% Nous en sommes là! Approches modernes Un autre angle d'attaque consiste à reporter le problème: trouver une théorie dont découlerait automatiquement la preuve de la conjecture de Riemann. c'est l'approche avec les fonctions de Möbius. Suite en Approches modernes En 2000, le Clay Mathematics Institute of Cambridge (Massachusetts) Cet Institut offre 1 million de dollars à quiconque pourra apporter une réponse à l'hypothèse de Riemann.

En 2013, Yitang Zhang (Université du New Hampshire – Durham): il existe une infinité de nombres premiers avec un intervalle de 70 millions.

En 2015, Le mathématicien James Maynard à l’université d’Oxford, au Royaume-Uni, a remporté la médaille Fields en 2022, entre autres pour avoir amélioré le résultat de Yitang Zhang en prouvant que la conjecture est vraie pour tout intervalle supérieur à 600, puis à 243.

En 2022, Yitang Zhang affirme avoir résolu une version faible de la conjecture de Landau-Siegel, équivalente à la célèbre conjecture de Riemann. Publication non encore approuvée.

Une façon de compter les nombres premiers est de les répartir en un nombre fini de groupes selon leurs congruences mod p, p étant un nombre premier. Par exemple, lorsque p = 5, les nombres premiers se répartissent en quatre groupes selon que le reste de leur division par p vaut 1, 2, 3 ou 4.

Cela est possible avec un échantillon de nombres premiers suffisamment grand; mais quelle est la taille de l'échantillon ? Sans doute très grand et augmentant exponentiellement avec p.

En 1936, Carl Ludwig Siegel, mathématicien allemand, a trouvé une formule relativement simple liée à ce problème de distribution des nombres premiers, qui rend les échantillons nécessaires potentiellement beaucoup plus petits.

Il a montré que si, dans certaines circonstances, sa formule ne donnait pas 0, cela revenait à prouver la conjecture. Edmund Landau ayant obtenu le même résultat, ce problème est devenu la conjecture des zéros de Landau-Siegel.

Ce que Yitang Zhang prétend avoir prouvé en est une version plus faible, mais qui aurait des conséquences similaires concernant la distribution des nombres premiers.

Source: Mathematician who solved prime-number riddle claims new breakthrough

– Nature – 11 nov 2022

Voir Brève 47-937

Suite	Zêta de Riemann Démonstration de l'identité d'Euler Approches modernes de la démonstration Fonction multiplicative lambda de Liouville
Voir	Calcul et calcul mental Divisibilité Euler – Index Géométrie – Index Identités remarquables Isopérimètre Nombres premiers Série Harmonique Théorie des nombres – Index
Site	Edmund Georg Hermann Landau
Vidéo	Cap sur l’hypothèse de Riemann | Voyages au pays des maths | ARTE
Livres	La symphonie des nombres premiers – Marcus du Sautoy – Points Science (Héloïse d'Ormesson) – 2005. Superbe! Livre de poche de 500 pages qui se lit comme un roman. Raconte toute cette recherche pour prouver la conjecture de Riemann tout en faisant quelques détours mathématiques intéressants. Appréciable aussi, l'atmosphère du monde des chercheurs en mathématiques. Karl Sabbagh – Dr. Riemann's zeros The search for the $ 1 million solution to the greatest problem in mathematics – Atlantic book London – 2003 L'ÉQUATION DE DIEU – Igor et Grichka Bogdanov – Grasset – 2019 – Bernhard Riemann avait découvert en 1859 une mystérieuse formule qui, selon ses propres mots, "indiquait le chemin qui mène vers Dieu". Cette page est citée dans ce livre pages 42 et 162.
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/Riemann.htm