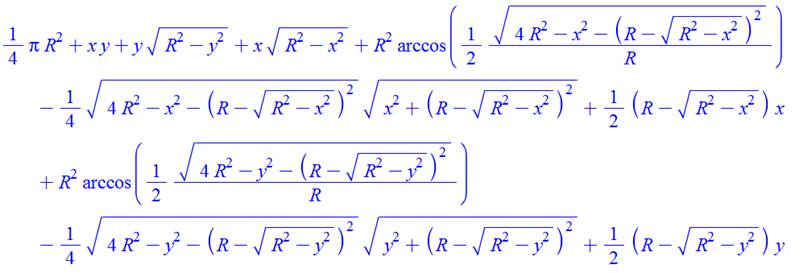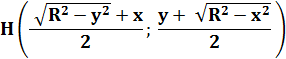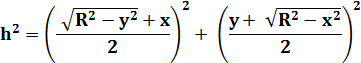|
||||||||||||||||||||||||||||||||||||||||
![]()
|
RECTANGLE et CERCLE Quatre quadrants
Attention, au fur et à
mesure que le rectangle glisse, il va dépasser le disque, créant un cas
particulier à analyser. |
|
|
|||
|
|
|||
|
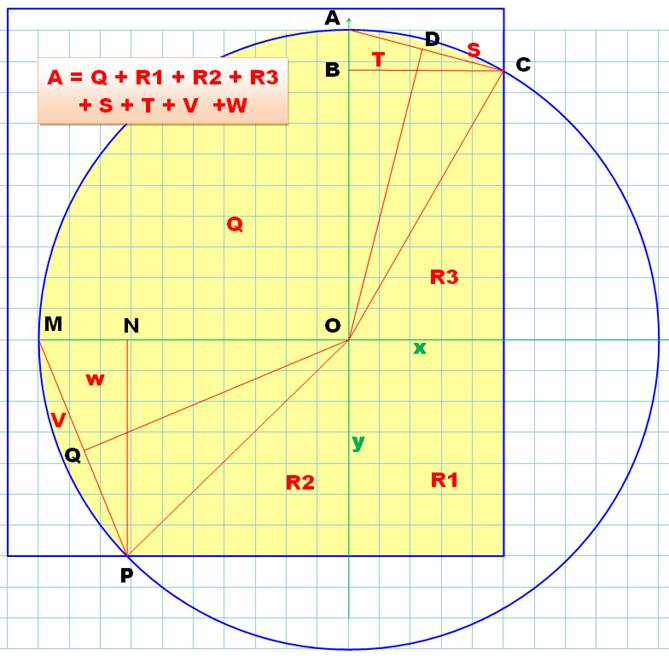
Aire du quadrant Q |
|
Q = 78,539… |
|
|
Aire du rectangle R1 |
|
R1 = 35 |
|
|
Dans le triangle ONP |
ON² = R² - y² |
ON = 7,14… |
|
|
Aire du rectangle R2 |
|
R2 = 49,99… |
|
|
Aire du triangle W |
|
W =10,00… |
|
|
Dans le triangle MNP |
|
MP = 7,56… |
|
|
Dans le triangle OMQ |
|
OQ = 9,26… |
|
|
Aire du segment V |
|
V = 3,77… |
|
|
Dans le triangle OBC |
OB² = R² - x² |
OB = 8,66… |
|
|
Aire du rectangle R3 |
|
R3 = 43,30… |
|
|
Aire du triangle T |
|
T = 3,35… |
|
|
Dans le triangle ABC |
|
AC = 5,17… |
|
|
Dans le triangle OAD |
|
k = 9,66… |
|
|
Aire du segment S |
|
S = 1,18… |
|
|
Aire totale A |
A = Q + R1 + R2 + R3 + S + T + V + W |
A = 225,13… |
|
|
Formule
complète
|
|||
|
|
|||
|
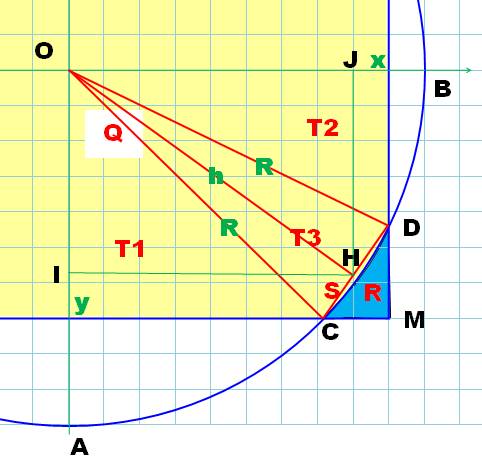
Lorsque le point M sort du
cercle il engendre un artefact (zone en bleu) qu'il s'agit de déduire du
calcul de l'aire interceptée. R
= Q – (T1 + T2 + T3 + S)
|
|||
|
Point
M |
M (x; y) |
M (9, 7) |
|
|
Point
C |
|
C (7,14…; 7) |
|
|
Point
D |
|
C (9; 4,36…) |
|
|
Milieu
de CD |
|
H (8,07…;
5,68…) |
|
|
Mesure
de OH |
|
h = 9,87… |
|
|
Mesure
de CD |
|
CD = 3,23… |
|
|
Aire
T1 |
|
T1 = 25,00… |
|
|
Aire
T2 |
|
T2 = 19,61… |
|
|
Aire
T3 |
|
T3 = 15,93… |
|
|
Aire
segment S |
|
S = 0,28 … |
|
|
Aire
rectangle Q |
|
Q = 63 |
|
|
Aire
à retirer R |
R = Q – (T1 + T2 + T3 + S) |
R = 2,17... |
|
Voir Abaque
|
Ce
cas ne se prête pas facilement aux calculs systématiques. Il nécessite une
condition. Si la distance de 0 au coin bas-droit M (x, y) du rectangle et supérieure
au rayon, alors retirez le petit bout qui dépasse. Cette condition s'exprime
par x² + y² > R². |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Rectang4.htm |
![]()