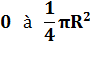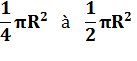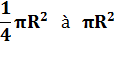|
||||||||||||||||||||||||||||||||||||||||
![]()
|
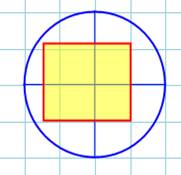
Calcul de l'aire de l'intersection du RECTANGLE avec le CERCLE
Ce calcul est toutefois
accessible à ceux qui connaissent les bases de la géométrie. Certains résolvent ce
problème en utilisant le calcul intégral sur
le cercle. Méthode
qui se prête bien à un calcul sur ordinateurs (programmation). Cette page fait le tour de la question. Les pages suivantes analysent
les configurations diverses. Une page est consacrée aux abaques pour un
disque de rayon de référence. |
Anglais Rectangle and
circle collision / overlap /
intersection
|
|
|
|
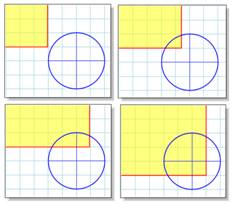
Nous nous intéressons au cas
d'un rectangle de grande dimension par rapport au cercle. Ce grand rectangle
glisse progressivement dans un cercle. Nous désirons connaître l'aire de la
partie commune au disque et au rectangle. Plusieurs cas de figure sont
à analyser. |
|
|
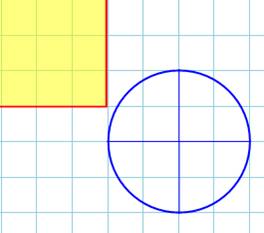
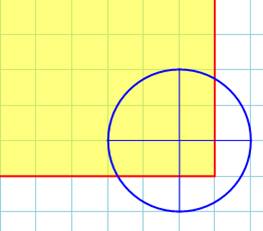
Le rectangle est extérieur
au cercle. L'intersection est naturellement vide. Nous précisons, à ce niveau, que ces représentations englobent toutes
les autres obtenues par rotation. |
|
|
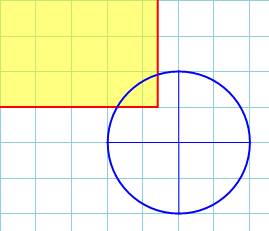
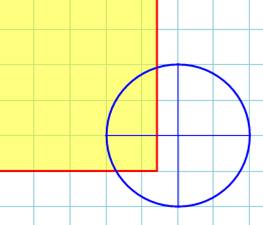
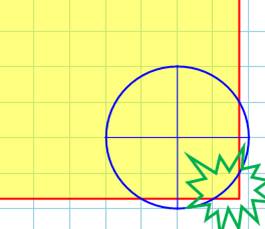
Premier cas intéressant, le
rectangle pénètre le premier quadrant du cercle. Selon sa position l'aire de
l'intersection varie de:
Suite un
quadrant |
|
|
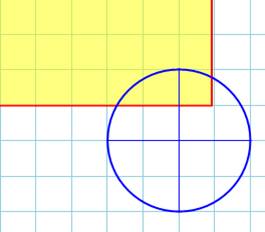
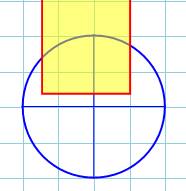
Deuxième cas, le rectangle
empiète sur le deuxième quadrant. L'aire varie de:
Suite deux quadrants |
|
|
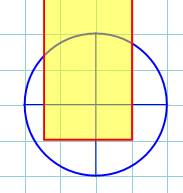
Intersection de deux
quadrants: mais, ce cas est équivalent au précédent par rotation et symétrie. |
|
|
Les quatre quadrants sont
impactés et l'aire varie de:
Jusqu'à englober le disque
entier. Suite quatre quadrants |
|
|
Un cas particulier. Ne pas
oublier de retirer ce petit morceau! Suite quatre quadrants |
|
|
Ces cas ne sont pas abordés,
mais ils sont facilement calculables en reprenant la méthode employée sur ces pages. |
|
|
Cas trivial où l'aire de
l'intersection est celle du rectangle |
|
|
Finalement
trois cas sont à considérer. Nous allons donner les calculs, les formules et
les abaques utiles pour ceux qui ne disposent pas
de logiciels de calcul. Une
méthode graphique parfois est parfois
largement suffisante. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Rectangl.htm |
![]()